junio 8, 2020
~ 7 MIN
Programación Orientada a Arrays
< Blog RSSProgramación Orientada a Arrays
En el post anterior introdujimos NumPy y varias de sus características principales. La principal ventaja que ofrece NumPy es la velocidad superior respecto a Python en aplicaciones que requieren estructuras de datos numéricas que podemos expresar en forma de vectores, matrices o tensores. Parte de esta mejora viene del hecho que usando NumPy podemos llevar a cabo muchos tipos de procesado de datos mediante expresiones concisas aplicadas sobre arrays que de otra forma requerirían loops. La práctica de sustituir loops por expresiones basadas en arrays se conoce como vectorización, que junto al broadcasting forman la base de la programación orientada a array (Array-Oriented Programming). En este post vamos a explicar estos conceptos para poder sacar el máximo provecho de NumPy y así obtener varios ordenes de magnitud en el speedup de nuestro código en Python.
Vectorización
Imaginad que queremos evaluar la función sobre una malla regular de valores. Una manera simple de llevar a cabo esta operación es la siguiente:
import numpy as np
import math
def lento(n=1000):
x = np.linspace(-1,1,n)
y = np.linspace(-1,1,n)
z = np.empty((n,n))
for i, _y in enumerate(y):
for j, _x in enumerate(x):
z[i, j] = math.sqrt(_x**2 + _y**2)
return x, y, z
%time x, y, z = lento()
Wall time: 909 ms
Podemos visualizar esta función usando Matplotlib (una librería sobre la que hablaremos en detalle en un futuro post).
import matplotlib.pyplot as plt
def plot(x, y, z):
plt.contourf(x, y, z)
plt.colorbar()
plt.xlabel("x", fontsize="16")
plt.ylabel("y", fontsize="16")
plt.title("$z = \sqrt{x^2 + y^2 }$", fontsize="16")
plt.show()
plot(x, y, z)

Como puedes ver en la implementación de la función la evaluación de la expresión requiere de dos bucles for para iterar sobre todos los valores de x e y calculando el resultado. Esta es una implementación ineficiente que puede acelerarse si aplicamos la vectorización, sustituir bucles por expresiones basadas en arrays.
def rapido(n=1000):
p = np.linspace(-1,1,n)
x, y = np.meshgrid(p, p)
z = np.sqrt(x**2 + y**2)
return x, y, z
%time x, y, z = rapido()
Wall time: 19 ms
plot(x, y, z)

El resultado que obtenemos es el mismo, pero 50 veces más rápido. Esto es gracias al uso de la vectorización. NumPy pone a nuestra disposición multitud de funciones que podemos aprovechar para acelerar nuestros cálculos.
Funciones Universales
Estas funciones llevan a cabo operaciones elemento a elemento en un array. En el ejemplo anterior ya hemos visto una de ellas, np.sqrt, para calcular la raíz cuadrada de todos los elementos en un array sin necesidad de implementar ningún bucle. Aquí tienes unos cuantos ejemplos.
a = np.array([[2.5, 3.1, 7], [10, 11, 12]])
a
array([[ 2.5, 3.1, 7. ],
[10. , 11. , 12. ]])
for func in (np.abs, np.sqrt, np.exp, np.log, np.sign, np.ceil, np.modf, np.isnan, np.cos):
print("\n", func.__name__)
print(func(a))
absolute
[[ 2.5 3.1 7. ]
[10. 11. 12. ]]
sqrt
[[1.58113883 1.76068169 2.64575131]
[3.16227766 3.31662479 3.46410162]]
exp
[[1.21824940e+01 2.21979513e+01 1.09663316e+03]
[2.20264658e+04 5.98741417e+04 1.62754791e+05]]
log
[[0.91629073 1.13140211 1.94591015]
[2.30258509 2.39789527 2.48490665]]
sign
[[1. 1. 1.]
[1. 1. 1.]]
ceil
[[ 3. 4. 7.]
[10. 11. 12.]]
modf
(array([[0.5, 0.1, 0. ],
[0. , 0. , 0. ]]), array([[ 2., 3., 7.],
[10., 11., 12.]]))
isnan
[[False False False]
[False False False]]
cos
[[-0.80114362 -0.99913515 0.75390225]
[-0.83907153 0.0044257 0.84385396]]
Funciones Estadísticas
Estas funciones nos van a permitir calcular valores estadísticos sobre nuestros arrays. Algunos ejemplos son
for func in (a.min, a.max, a.sum, a.prod, a.std, a.var):
print(func.__name__, "=", func())
min = 2.5
max = 12.0
sum = 45.6
prod = 71610.0
std = 3.7260345319566395
var = 13.883333333333333
También podemos especificar la dimensión sobre la que queremos calcular estos valores de la siguiente manera
# calcular valor medio de cada columna
a.mean(axis=0)
array([6.25, 7.05, 9.5 ])
# suma todos los valores de cada fila
a.sum(axis=1)
array([12.6, 33. ])
Broadcasting
El broadcasting es la segunda propiedad (después de la vectorización) que le proporciona a NumPy su versatilidad y potencia a la hora de llevar a cabo operaciones con arrays. Como norma general, cuando Numpy espera arrays de la misma forma pero encuentra que esto no se cumple aplica las reglas del broadcasting. Vamos a verlas en detalle.
Primera regla
Si dos arrays no tienen el mismo rango, entonces se añadirá una dimensión de 1 al principio del array con menor rango hasta que éstos coincidan.
💡 El rango de un
arrayes lo mismo que su numero de dimensiones.
Vamos a crear un array de 3 dimensiones.
a = np.arange(5).reshape(1, 1, 5)
a
array([[[0, 1, 2, 3, 4]]])
a.shape
(1, 1, 5)
Ahora, vamos a sumarle otro array de una sola dimension.
b = np.arange(5)
b
array([0, 1, 2, 3, 4])
b.shape
(5,)
a + b
array([[[0, 2, 4, 6, 8]]])
Como puedes ver, NumPy no se ha quejado ni nos ha dado ningún error pese a que formalmente esta operación no es válida. Lo que ha ocurrido es que la primera regla del broadcasting ha sido aplicada, añadiendo dimensiones extra a nuestro array b para convertirlo en una array con dimensiones (1, 1, 5) y así poder llevar a cabo la operación. Esta es la misma regla que nos permite sumar un valor escalar a un vector o una matriz.
1 + a
array([[[1, 2, 3, 4, 5]]])
Seguna regla
Si un array tiene un 1 en alguna dimensión en particular actuará como si tuviese la longitud del array con mayor longitud en aquella dimensión. Esto implica que el valor en esta dimensión se repetirá hasta coincidir con la longitud. Por ejemplo
a = np.arange(6).reshape(2, 3)
a
array([[0, 1, 2],
[3, 4, 5]])
a.shape
(2, 3)
b = np.array([[100], [200]])
b
array([[100],
[200]])
b.shape
(2, 1)
Si intentamos sumar estas dos matrices, NumPy repetirá los valores de b hasta crear tres columnas iguales y así poder llevar a cabo la operación.
a + b
array([[100, 101, 102],
[203, 204, 205]])
Las reglas pueden combinares, por ejemplo
c = np.array([100, 200, 300])
c.shape
(3,)
a + c
array([[100, 201, 302],
[103, 204, 305]])
NumPy ha añadido una dimensión extra al principio de c para obtener una forma de (1, 3) y luego ha repetido todos los valores en una nueva fila para obtener una forma de (2, 3) y así poder llevar a cabo la suma.
Tercera regla
Después de aplicar las reglas 1 y 2, las dimensiones de los arrays deben coincidir. Si no es así, la operación no se puede llevar a cabo.
a + [1, 2]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-82-5e6b24fb2d02> in <module>
----> 1 a + [1, 2]
ValueError: operands could not be broadcast together with shapes (2,3) (2,)
Aquí tienes un ejemplo visual de estas reglas aplicadas sobre varios arrays.
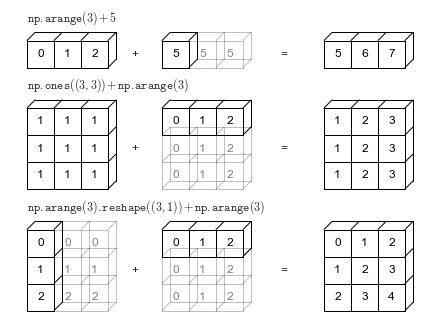
Estas reglas se aplican en prácticamente todas las operaciones de NumPy que requieran dos arrays, no solo operaciones aritméticas. Ser capaces de utilizar el broadcasting a nuestro favor nos ayudará en la implementación de algoritmos rápidos y eficientes.
Resumen
En este post hemos hablado sobre programación orientada a arrays, un concepto que puede dar como resultado código más rápido y conciso. Este paradigma de programación está basado en la idea de sustituir lentos bucles por operaciones basadas en arrays para el procesado de datos. Esta idea se conoce como vectorización. En Python, utilizamos NumPy y sus funciones para conseguir acelerar nuestro código. Una propiedad clave a la hora de conseguir estos resultados es el broadcasting que nos permitirá vectorizar nuestro código incluso en aquellas ocasiones en las que, estrictamente hablando, no podríamos (por ejemplo para sumar dos matrices con diferentes dimensiones). Entender estas propiedades y saber aprovecharlas es clave para conseguir implementar algoritmos rápidos y eficientes, algo que utilizaremos de manera extensiva en el análisis de datos y la implementación de algoritmos de Inteligencia Artificial.