Receta para entrenar Redes Neuronales

En posts anteriores hemos introducido muchos conceptos que nos pueden ayudar a la hora de entrenar redes neuronales de manera efectiva, consiguiendo buenas prestaciones. En este post vamos a presentar una receta sencilla que puedes seguir para empezar a entrenar tus redes aplicando las prácticas más comunes con el objetivo de minimizar la posibilidad de introducir errores en el proceso.

Exploración de Datos

Cualquier proyecto de Machine Learning empieza siempre con una fase de exploración de datos. Estas son algunas de las preguntas que deberías responder antes de ponerte a entrenar ningún modelo:

• Tipo de problema: regresión, clasificación (binaria, multiclase, ...), ...
• Número de clases (clasificación) o valores a predecir (regresión)
• Distribución de clases

En este ejemplo seguiremos trabajando con el dataset CIFAR10 para clasificación de imágenes, por lo que también nos interesa:

• Visualizar imágenes
• Número de canales (gris, color, multi-espectral, ...)
• Resolución (alto y ancho)
• Estadísticos (mean/std, max/min, ...)
• Tipo de datos (unit8, float16, ...)

Y cualquier otro aspecto que sea relevante.

import torchvision

trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True)

testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True)

classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

len(trainset), len(testset)

Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data\cifar-10-python.tar.gz



HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value='')))


Extracting ./data\cifar-10-python.tar.gz to ./data
Files already downloaded and verified





(50000, 10000)

# visualizción imágenes

import random
import matplotlib.pyplot as plt

r, c = 3, 5
plt.figure(figsize=(c*3, r*3))
for row in range(r):
    for col in range(c):
        index = c*row + col
        plt.subplot(r, c, index + 1)
        ix = random.randint(0, len(trainset)-1)
        img, label = trainset[ix]
        plt.imshow(img)
        plt.axis('off')
        plt.title(classes[label])
plt.subplots_adjust(wspace=0.2, hspace=0.5)
plt.show()

# convertimos imágenes a arrays de numpy

import numpy as np

train_images = np.array([np.array(img) for img, label in trainset])
test_images = np.array([np.array(img) for img, label in testset])

train_labels = np.array([label for img, label in trainset])
test_labels = np.array([label for img, label in testset])

# ver número de imágenes, resolución y número de canales

train_images.shape, test_images.shape, train_labels.shape, test_labels.shape

((50000, 32, 32, 3), (10000, 32, 32, 3), (50000,), (10000,))

# tipo de datos

train_images.dtype, train_labels.dtype

(dtype('uint8'), dtype('int32'))

# estadísiticos

max_value = train_images.max(axis=(0, 1, 2))
min_value = train_images.min(axis=(0, 1, 2))

max_value, min_value

(array([255, 255, 255], dtype=uint8), array([0, 0, 0], dtype=uint8))

mean = (train_images / 255).mean(axis=(0, 1, 2))
std = (train_images / 255).std(axis=(0, 1, 2))

mean, std

(array([0.49139968, 0.48215841, 0.44653091]),
 array([0.24703223, 0.24348513, 0.26158784]))

# distribución de clases

plt.hist(train_labels, bins=len(classes))
plt.show()

unique, counts = np.unique(train_labels, return_counts=True)
unique, counts

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
 array([5000, 5000, 5000, 5000, 5000, 5000, 5000, 5000, 5000, 5000],
       dtype=int64))

En este caso nuestro dataset está balanceado (tenemos el mismo número de muestras por cada clase). En ocasiones, éste no será el caso. Entrenar un modelo con un dataset desbalanceado introducirá bias, haciendo que nuestro modelo sea más propenso a predecir las clases más presentes. Para solventar este problema existen varias opciones, la más común es sobre-muestrear las clases menos representadas (combinado con data augmentation puede ser especialmente positivo).

Una vez conocemos bien nuestros datos, podemos empezar a trabajar en nuestra red neuronal. Sin embargo, antes de entrenarla en todo nuestro dataset será muy positivo seguir antes los siguiente pasos.

Validando nuestra red neuronal

Digamos que decidimos usar una arquitectura de MLP para resolver nuestro problema.

import torch

def build_model(D_in=32*32*3, H=100, D_out=10):
    return torch.nn.Sequential(
        torch.nn.Linear(D_in, H),
        torch.nn.ReLU(),
        torch.nn.Linear(H, H),
        torch.nn.ReLU(),
        torch.nn.Linear(H, D_out)
    ).cuda()

Una muy buena manera de asegurarnos que nuestra red hace lo que debería es pasarle como entrada un tensor con las dimensiones esperadas durante el entrenamiento y asegurarnos que la salida que nos da coincide también con lo que esperamos. En nuestro caso, enviaremos tensores que contendrán un número determinado de imágenes (un batch, por ejemplo 64) y cada imagen estará representada por un vector de $32323$ valores. La salida debería ser un vector de 10 valores para cada imagen del batch representando la probabilidad de cada clase.

model = build_model()
test_input = torch.randn((64, 32*32*3)).cuda()
test_output = model(test_input)
test_output.shape

torch.Size([64, 10])

Si cometemos algún error definiendo nuestra red neuronal, en este paso lo podríamos detectar (en esta caso el MLP es una arquitectura muy sencilla, pero con redes neuronales grandes es muy fácil cometer errores a la hora de definir las dimensiones de cada capa).

Fit de una muestra

Una vez nos hemos asegurado que las dimensiones de nuestra red están bien, el siguiente paso es asegurarnos de que es capaz de aprenderse de memoria una sola muestra del dataset. Si este no es el caso podemos estar seguros de que algo no anda bien.

import numpy as np

train_images = np.array([np.array(img) for img, label in trainset])
X_test = np.array([np.array(img) for img, label in testset])

train_labels = np.array([label for img, label in trainset])
y_test = np.array([label for img, label in testset])

X_train, X_val, X_subset = train_images[:40000], train_images[40000:], train_images[:5000]
y_train, y_val, y_subset = train_labels[:40000], train_labels[40000:], train_labels[:5000]

X_train.shape, X_val.shape, X_test.shape, X_subset.shape

((40000, 32, 32, 3), (10000, 32, 32, 3), (10000, 32, 32, 3), (5000, 32, 32, 3))

class Dataset(torch.utils.data.Dataset):
    def __init__(self, X, Y):
        self.X = torch.from_numpy(X / 255.).float().cuda().view(-1, 32*32*3)
        self.Y = torch.from_numpy(Y).long().cuda()
    def __len__(self):
        return len(self.X)
    def __getitem__(self, ix):
        return self.X[ix], self.Y[ix]

# fit de la primera imagen del dataset

dataset = Dataset(X_subset[:1], y_subset[:1])
dataloader = torch.utils.data.DataLoader(dataset, batch_size=1)

len(dataset)

1

epochs = 3
criterion = torch.nn.CrossEntropyLoss()
model = build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
for e in range(1, epochs+1):
    for x_b, y_b in dataloader:
        y_pred = model(x_b)
        loss = criterion(y_pred, y_b)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        print(f"Epoch {e}/{epochs} loss {loss.item():.5f} y {y_b.item()} y_pred {torch.argmax(y_pred, axis=1).item()}")

Epoch 1/3 loss 2.33693 y 6 y_pred 1
Epoch 2/3 loss 0.00748 y 6 y_pred 6
Epoch 3/3 loss 0.00000 y 6 y_pred 6

Podemos hacer el fit de una imagen sin problema. Errores como una función de pérdida incorrecta o diferentes dimensiones entre las predicciones y las etiquetas podrían ser detectados en este paso.

Fit de un batch

Siguiendo la misma lógica, nuestro modelo debería ser capaz de aprenderse de memoria un solo batch de imágenes.

# fit de un batch

dataset = Dataset(X_subset[:64], y_subset[:64])
dataloader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True)

len(dataset)

64

epochs = 100
criterion = torch.nn.CrossEntropyLoss()
model = build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
for e in range(1, epochs+1):
    for x_b, y_b in dataloader:
        y_pred = model(x_b)
        loss = criterion(y_pred, y_b)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        acc = (y_b == torch.argmax(y_pred, axis=1)).sum().item()
        if not e % 10:
            print(f"Epoch {e}/{epochs} loss {loss.item():.5f} acc {acc}/{y_b.shape[0]}")

Epoch 10/100 loss 2.19237 acc 13/64
Epoch 20/100 loss 1.82428 acc 25/64
Epoch 30/100 loss 1.12995 acc 41/64
Epoch 40/100 loss 0.52760 acc 56/64
Epoch 50/100 loss 0.17038 acc 63/64
Epoch 60/100 loss 0.04260 acc 64/64
Epoch 70/100 loss 0.01039 acc 64/64
Epoch 80/100 loss 0.00431 acc 64/64
Epoch 90/100 loss 0.00264 acc 64/64
Epoch 100/100 loss 0.00194 acc 64/64

En este punto ya podemos estar bastante seguros de que nuestro modelo está bien definido, estamos usando la función de pérdida y optimizador adecuados, nuestro bucle de entrenamiento funciona bien, etc.

Entrenando con un sub-conjunto de datos

Entrenar una red neuronal en un dataset completo puede ser computacionalmente costoso si el dataset es muy grande. Esto implica que si queremos hacer pruebas para probar diferentes combinaciones de hyperparámetros vamos a tener que esperar mucho tiempo, o alquilar grandes clusters de GPUs (lo cual es muy caro). Una solución es iterar utilizando un sub-conjunto representativo de nuestro dataset, confiando en que las conclusiones a las que lleguemos en este pequeño conjunto luego se transfieran a todo el dataset.

dataset = {
    'train': Dataset(X_subset, y_subset),
    'val': Dataset(X_val, y_val),
}

dataloader = {
    'train': torch.utils.data.DataLoader(dataset['train'], batch_size=32, shuffle=True),
    'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
}

len(dataset['train']), len(dataset['val'])

(5000, 10000)

from sklearn.metrics import accuracy_score

def softmax(x):
    return torch.exp(x) / torch.exp(x).sum(axis=-1,keepdims=True)

def fit(model, dataloader, optimizer, scheduler=None, epochs=10, log_each=1, weight_decay=0, early_stopping=0, verbose=1):
    criterion = torch.nn.CrossEntropyLoss()
    l, acc, lr = [], [], []
    val_l, val_acc = [], []
    best_acc, step = 0, 0
    for e in range(1, epochs+1):
        _l, _acc = [], []
        for param_group in optimizer.param_groups:
            lr.append(param_group['lr'])
        model.train()
        for x_b, y_b in dataloader['train']:
            y_pred = model(x_b)
            loss = criterion(y_pred, y_b)
            _l.append(loss.item())
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            y_probas = torch.argmax(softmax(y_pred), axis=1)
            _acc.append(accuracy_score(y_b.cpu().numpy(), y_probas.cpu().detach().numpy()))
        l.append(np.mean(_l))
        acc.append(np.mean(_acc))
        model.eval()
        _l, _acc = [], []
        with torch.no_grad():
            for x_b, y_b in dataloader['val']:
                y_pred = model(x_b)
                loss = criterion(y_pred, y_b)
                _l.append(loss.item())
                y_probas = torch.argmax(softmax(y_pred), axis=1)
                _acc.append(accuracy_score(y_b.cpu().numpy(), y_probas.cpu().numpy()))
        val_l.append(np.mean(_l))
        val_acc.append(np.mean(_acc))
        # guardar mejor modelo
        if val_acc[-1] > best_acc:
            best_acc = val_acc[-1]
            torch.save(model.state_dict(), 'ckpt.pt')
            step = 0
            if verbose == 2:
                print(f"Mejor modelo guardado con acc {best_acc:.5f} en epoch {e}")
        step += 1
        if scheduler:
            scheduler.step()
        # parar
        if early_stopping and step > early_stopping:
            print(f"Entrenamiento detenido en epoch {e} por no mejorar en {early_stopping} epochs seguidas")
            break
        if not e % log_each and verbose:
            print(f"Epoch {e}/{epochs} loss {l[-1]:.5f} acc {acc[-1]:.5f} val_loss {val_l[-1]:.5f} val_acc {val_acc[-1]:.5f} lr {lr[-1]:.5f}")
    # cargar mejor modelo
    model.load_state_dict(torch.load('ckpt.pt'))
    return {'epoch': list(range(1, len(l)+1)), 'loss': l, 'acc': acc, 'val_loss': val_l, 'val_acc': val_acc, 'lr': lr}

Por ejemplo, de la siguiente manera podríamos elegir un learning rate adecuado.

lrs = [0.01, 0.001, 0.0001]
hists = []
for lr in lrs:
    print(f"Probando lr {lr}")
    model = build_model()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    hist = fit(model, dataloader, optimizer, epochs=10, verbose=0)
    hists.append(hist)

# tarda 12 segundos

Probando lr 0.01
Probando lr 0.001
Probando lr 0.0001

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(121)
for i in range(len(lrs)):
    ax.plot(hists[i]['loss'], label=lrs[i])
ax.legend()
ax.grid(True)
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
ax = plt.subplot(122)
for i in range(len(lrs)):
    ax.plot(hists[i]['val_acc'], label=lrs[i])
ax.legend()
ax.grid(True)
ax.set_ylabel('acc')
ax.set_xlabel('epoch')
plt.show()

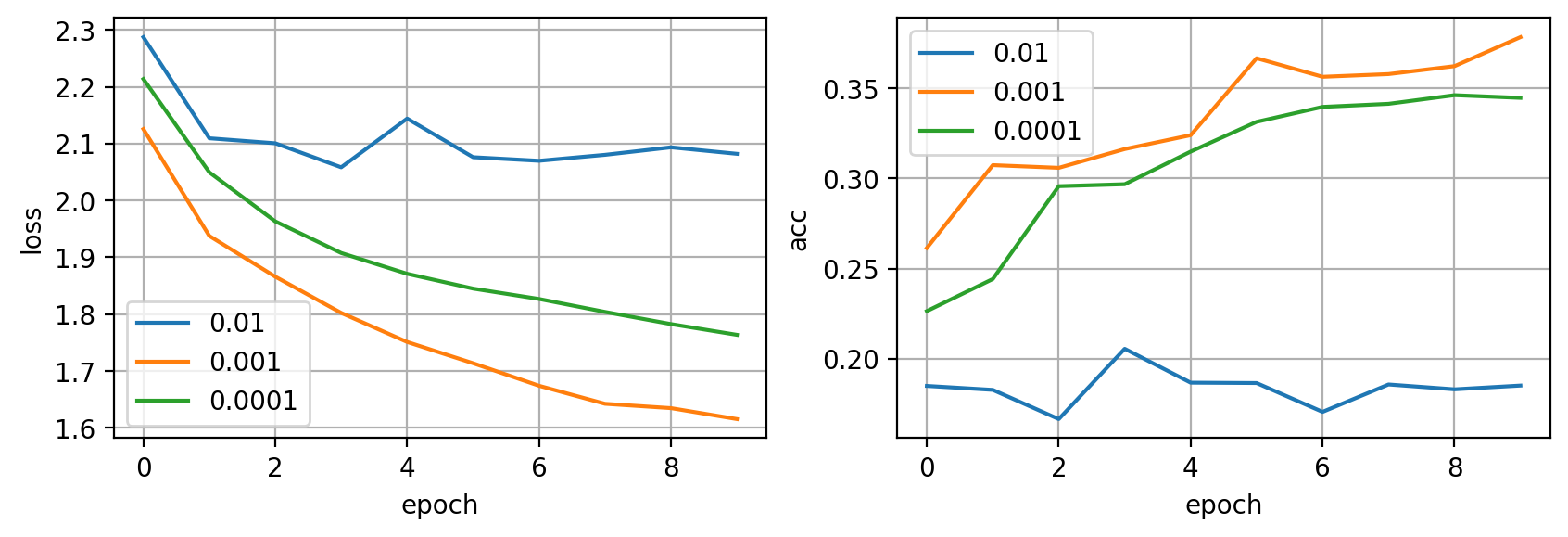
Parece que el valor intermedio de 0.001 nos da los mejores resultados en este caso. Ahora repetimos el experimento con todos los datos.

dataset = {
    'train': Dataset(X_train, y_train),
    'val': Dataset(X_val, y_val),
}

dataloader = {
    'train': torch.utils.data.DataLoader(dataset['train'], batch_size=32, shuffle=True),
    'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
}

len(dataset['train']), len(dataset['val'])

(40000, 10000)

hists = []
for lr in lrs:
    print(f"Probando lr {lr}")
    model = build_model()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    hist = fit(model, dataloader, optimizer, epochs=10, verbose=0)
    hists.append(hist)

# tarda 1 minuto y 17 segundos

Probando lr 0.01
Probando lr 0.001
Probando lr 0.0001

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(121)
for i in range(len(lrs)):
    ax.plot(hists[i]['loss'], label=lrs[i])
ax.legend()
ax.grid(True)
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
ax = plt.subplot(122)
for i in range(len(lrs)):
    ax.plot(hists[i]['val_acc'], label=lrs[i])
ax.legend()
ax.grid(True)
ax.set_ylabel('acc')
ax.set_xlabel('epoch')
plt.show()

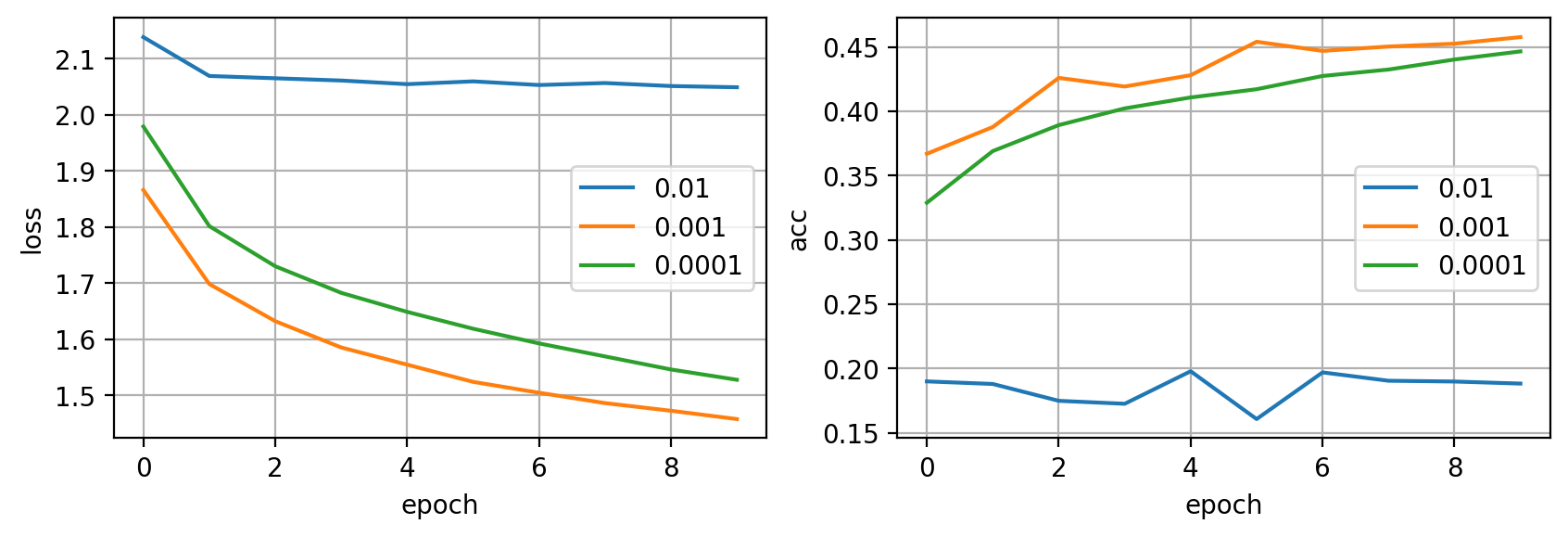
Obtenemos el mismo resultado, pero necesitando mucho más tiempo y cálculo. Así pues, experimentar rápidamente en un subconjunto representativo nos puede dar una gran ventaja.

Configuraciones recomendadas

Es fácil verse sobrepasado por el gran número de opciones que tenemos disponibles a la hora de entrenar nuestras redes, y obviamente no podemos probar todas las posibles combinaciones. Lo que podemos hacer es basarnos en el trabajo llevado a cabo por otros y utilizar sus resultados para empezar a trabajar. Estos son algunos buenos valores iniciales que puedes usar.

Batch Size

Valores recomendados son: 16, 32, 64. Puedes empezar por estos valores y luego experimentar con otros. Aún así, la tendencia es intentar utilizar el batch size más grande posible que quepa en la memoria de la GPU (o GPUs) y adaptar el learning rate para obtener un buen entrenamiento.

bss = [16, 32, 64]
hists = []
for bs in bss:
    print(f"Probando bs {bs}")
    dataloader = {
        'train': torch.utils.data.DataLoader(dataset['train'], batch_size=bs, shuffle=True),
        'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
    }
    model = build_model()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
    hist = fit(model, dataloader, optimizer, epochs=10, verbose=0)
    hists.append(hist)

Probando bs 16
Probando bs 32
Probando bs 64

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(121)
for i in range(len(bss)):
    ax.plot(hists[i]['loss'], label=bss[i])
ax.legend()
ax.grid(True)
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
ax = plt.subplot(122)
for i in range(len(bss)):
    ax.plot(hists[i]['val_acc'], label=bss[i])
ax.legend()
ax.grid(True)
ax.set_ylabel('acc')
ax.set_xlabel('epoch')
plt.show()

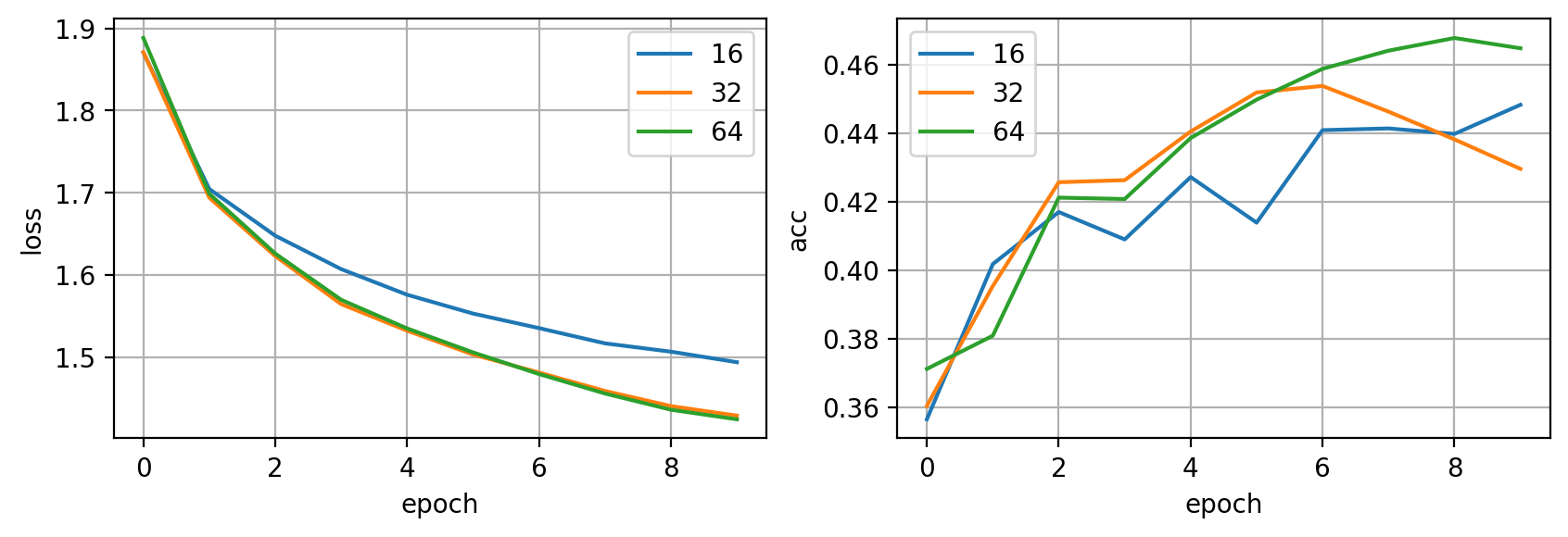
Optimizador y learning rate

Un buena combinación inicial es el optimizador Adam con un learning rate de . A partir de aquí puede experimentar con otros valores para sacar un extra de performance, pero estos valores suelen ser buenos para empezar.

Regularización

Cuando trabajamos con imágenes, utilizar data augmentation y batch norm es muy aconsejable para obtener buenos resultados. Combinándolo con early stopping seremos capaces de maneter el overfitting a raya. Puedes usar Weight decay si utilizas el optimizador SGD para regularizar mnás tu modelo, e incluso probar Dropout (sobretodo en arquitecturas de tipo MLP, no tanto en redes convolucionales).

def build_model(D_in=32*32*3, H=100, D_out=10):
    return torch.nn.Sequential(
        torch.nn.Linear(D_in, H),
        torch.nn.BatchNorm1d(H),
        torch.nn.ReLU(),
        torch.nn.Linear(H, H),
        torch.nn.BatchNorm1d(H),
        torch.nn.ReLU(),
        torch.nn.Linear(H, D_out)
    ).cuda()

from albumentations import Compose, RandomCrop, Resize, HorizontalFlip, ToGray, RGBShift, OneOf

trans = Compose([
    RandomCrop(24,24),
    Resize(32, 32),
    HorizontalFlip(),
    OneOf([
        ToGray(p=0.2),
        RGBShift(p=0.3)
    ])
])

class Dataset(torch.utils.data.Dataset):
    def __init__(self, X, Y, trans=None):
        self.X = X
        self.Y = Y
        self.trans = trans
    def __len__(self):
        return len(self.X)
    def __getitem__(self, ix):
        img = self.X[ix]
        if self.trans:
            img = trans(image=img)["image"]
        img = torch.from_numpy(img / 255.).float().cuda().view(-1)
        label = torch.tensor(self.Y[ix]).long().cuda()
        return img, label

dataset = {
    'train': Dataset(X_subset, y_subset, trans=trans),
    'val': Dataset(X_val, y_val),
}

dataloader = {
    'train': torch.utils.data.DataLoader(dataset['train'], batch_size=64, shuffle=True),
    'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
}

len(dataset['train']), len(dataset['val'])

(5000, 10000)

model = build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
hist = fit(model, dataloader, optimizer, epochs=100, early_stopping=10, verbose=2)

Mejor modelo guardado con acc 0.27900 en epoch 1
Epoch 1/100 loss 2.05086 acc 0.25534 val_loss 1.96951 val_acc 0.27900 lr 0.00100
Mejor modelo guardado con acc 0.30820 en epoch 2
Epoch 2/100 loss 1.94703 acc 0.29153 val_loss 1.94245 val_acc 0.30820 lr 0.00100
Mejor modelo guardado con acc 0.32480 en epoch 3
Epoch 3/100 loss 1.88550 acc 0.31784 val_loss 1.87018 val_acc 0.32480 lr 0.00100
Mejor modelo guardado con acc 0.33860 en epoch 4
Epoch 4/100 loss 1.84840 acc 0.32397 val_loss 1.84268 val_acc 0.33860 lr 0.00100
Mejor modelo guardado con acc 0.34800 en epoch 5
Epoch 5/100 loss 1.83081 acc 0.33584 val_loss 1.79098 val_acc 0.34800 lr 0.00100
Epoch 6/100 loss 1.80107 acc 0.35047 val_loss 1.79144 val_acc 0.34790 lr 0.00100
Mejor modelo guardado con acc 0.34950 en epoch 7
Epoch 7/100 loss 1.76621 acc 0.35839 val_loss 1.78763 val_acc 0.34950 lr 0.00100
Mejor modelo guardado con acc 0.36150 en epoch 8
Epoch 8/100 loss 1.75923 acc 0.36847 val_loss 1.76034 val_acc 0.36150 lr 0.00100
Mejor modelo guardado con acc 0.37010 en epoch 9
Epoch 9/100 loss 1.74236 acc 0.37184 val_loss 1.75802 val_acc 0.37010 lr 0.00100
Mejor modelo guardado con acc 0.38500 en epoch 10
Epoch 10/100 loss 1.72896 acc 0.38113 val_loss 1.76949 val_acc 0.38500 lr 0.00100
Epoch 11/100 loss 1.72198 acc 0.37935 val_loss 1.73932 val_acc 0.37580 lr 0.00100
Epoch 12/100 loss 1.70099 acc 0.38983 val_loss 1.81787 val_acc 0.35770 lr 0.00100
Epoch 13/100 loss 1.69687 acc 0.39695 val_loss 1.78855 val_acc 0.36590 lr 0.00100
Epoch 14/100 loss 1.68420 acc 0.39834 val_loss 1.75458 val_acc 0.36990 lr 0.00100
Epoch 15/100 loss 1.68568 acc 0.38805 val_loss 1.71205 val_acc 0.38050 lr 0.00100
Mejor modelo guardado con acc 0.38690 en epoch 16
Epoch 16/100 loss 1.68493 acc 0.40071 val_loss 1.73234 val_acc 0.38690 lr 0.00100
Epoch 17/100 loss 1.64198 acc 0.41080 val_loss 1.74442 val_acc 0.38040 lr 0.00100
Epoch 18/100 loss 1.63359 acc 0.41495 val_loss 1.73751 val_acc 0.37790 lr 0.00100
Epoch 19/100 loss 1.63031 acc 0.40941 val_loss 1.72322 val_acc 0.38320 lr 0.00100
Mejor modelo guardado con acc 0.39920 en epoch 20
Epoch 20/100 loss 1.65450 acc 0.39616 val_loss 1.67122 val_acc 0.39920 lr 0.00100
Epoch 21/100 loss 1.64548 acc 0.40309 val_loss 1.77408 val_acc 0.36520 lr 0.00100
Epoch 22/100 loss 1.61477 acc 0.42286 val_loss 1.70121 val_acc 0.39320 lr 0.00100
Mejor modelo guardado con acc 0.40500 en epoch 23
Epoch 23/100 loss 1.61226 acc 0.41515 val_loss 1.67924 val_acc 0.40500 lr 0.00100
Epoch 24/100 loss 1.63156 acc 0.41297 val_loss 1.78690 val_acc 0.37350 lr 0.00100
Epoch 25/100 loss 1.60350 acc 0.42623 val_loss 1.73924 val_acc 0.37920 lr 0.00100
Epoch 26/100 loss 1.59182 acc 0.41950 val_loss 1.72632 val_acc 0.39740 lr 0.00100
Epoch 27/100 loss 1.58880 acc 0.42662 val_loss 1.68684 val_acc 0.39580 lr 0.00100
Epoch 28/100 loss 1.59462 acc 0.43117 val_loss 1.72454 val_acc 0.38330 lr 0.00100
Epoch 29/100 loss 1.57588 acc 0.43453 val_loss 1.70531 val_acc 0.39460 lr 0.00100
Mejor modelo guardado con acc 0.41870 en epoch 30
Epoch 30/100 loss 1.59036 acc 0.43038 val_loss 1.64008 val_acc 0.41870 lr 0.00100
Epoch 31/100 loss 1.58305 acc 0.42860 val_loss 1.75490 val_acc 0.37900 lr 0.00100
Epoch 32/100 loss 1.59160 acc 0.42939 val_loss 1.67232 val_acc 0.40970 lr 0.00100
Epoch 33/100 loss 1.56460 acc 0.44343 val_loss 1.65348 val_acc 0.41400 lr 0.00100
Epoch 34/100 loss 1.58000 acc 0.43157 val_loss 1.66558 val_acc 0.41080 lr 0.00100
Epoch 35/100 loss 1.56686 acc 0.43315 val_loss 1.63972 val_acc 0.41830 lr 0.00100
Epoch 36/100 loss 1.56192 acc 0.43631 val_loss 1.64798 val_acc 0.41390 lr 0.00100
Mejor modelo guardado con acc 0.42810 en epoch 37
Epoch 37/100 loss 1.56316 acc 0.43236 val_loss 1.63196 val_acc 0.42810 lr 0.00100
Epoch 38/100 loss 1.56592 acc 0.43790 val_loss 1.71177 val_acc 0.39590 lr 0.00100
Mejor modelo guardado con acc 0.43400 en epoch 39
Epoch 39/100 loss 1.54393 acc 0.44146 val_loss 1.62078 val_acc 0.43400 lr 0.00100
Epoch 40/100 loss 1.55366 acc 0.43770 val_loss 1.63666 val_acc 0.41790 lr 0.00100
Epoch 41/100 loss 1.52876 acc 0.45194 val_loss 1.72256 val_acc 0.38430 lr 0.00100
Epoch 42/100 loss 1.52123 acc 0.44660 val_loss 1.65236 val_acc 0.41990 lr 0.00100
Epoch 43/100 loss 1.54225 acc 0.44244 val_loss 1.67376 val_acc 0.41210 lr 0.00100
Epoch 44/100 loss 1.52297 acc 0.44996 val_loss 1.68484 val_acc 0.40620 lr 0.00100
Epoch 45/100 loss 1.51162 acc 0.44877 val_loss 1.64861 val_acc 0.42890 lr 0.00100
Epoch 46/100 loss 1.50298 acc 0.45827 val_loss 1.69331 val_acc 0.41350 lr 0.00100
Epoch 47/100 loss 1.51562 acc 0.45174 val_loss 1.62791 val_acc 0.41570 lr 0.00100
Epoch 48/100 loss 1.51710 acc 0.45115 val_loss 1.67497 val_acc 0.41170 lr 0.00100
Entrenamiento detenido en epoch 49 por no mejorar en 10 epochs seguidas

import pandas as pd

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(121)
pd.DataFrame(hist).plot(x='epoch', y=['loss', 'val_loss'], grid=True, ax=ax)
ax = plt.subplot(122)
pd.DataFrame(hist).plot(x='epoch', y=['acc', 'val_acc'], grid=True, ax=ax)
plt.show()

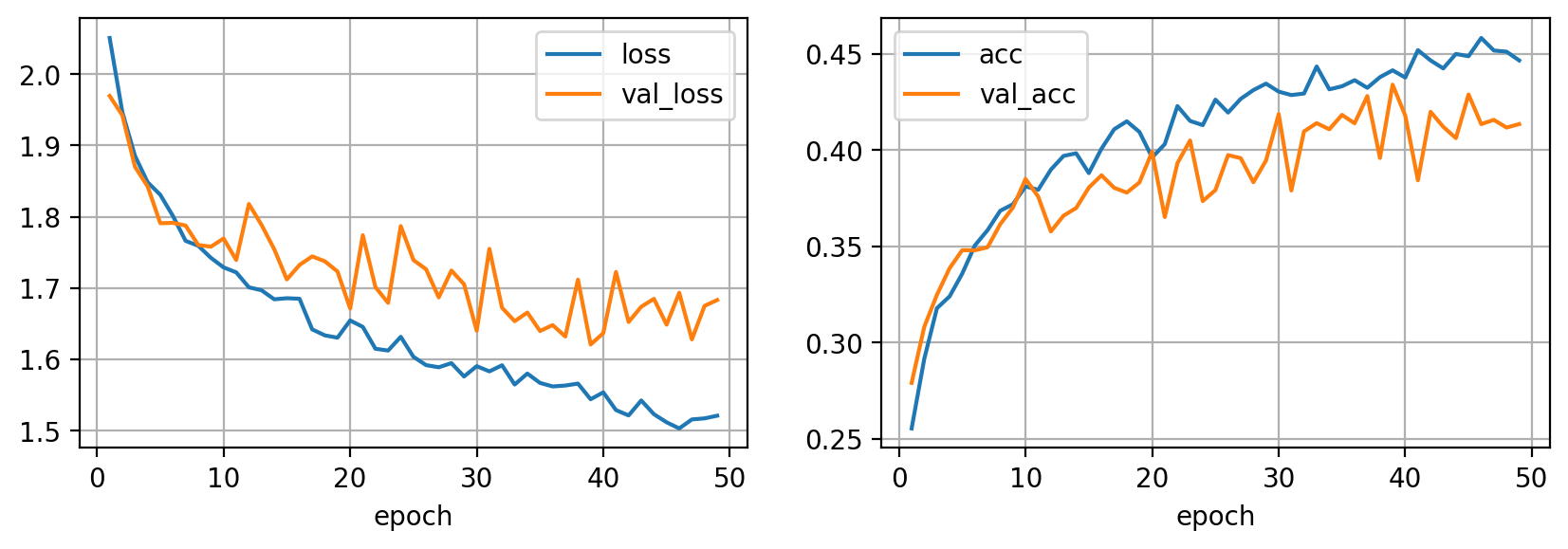
Puedes usar tu subset para experimentar rápidamente diferentes combinaciones de transformaciones para encontrar la mejor para tu caso en particular (aunque la opción por defecto es utilizar cuántas más, mejor).

Tuneado de Hyperparámetros

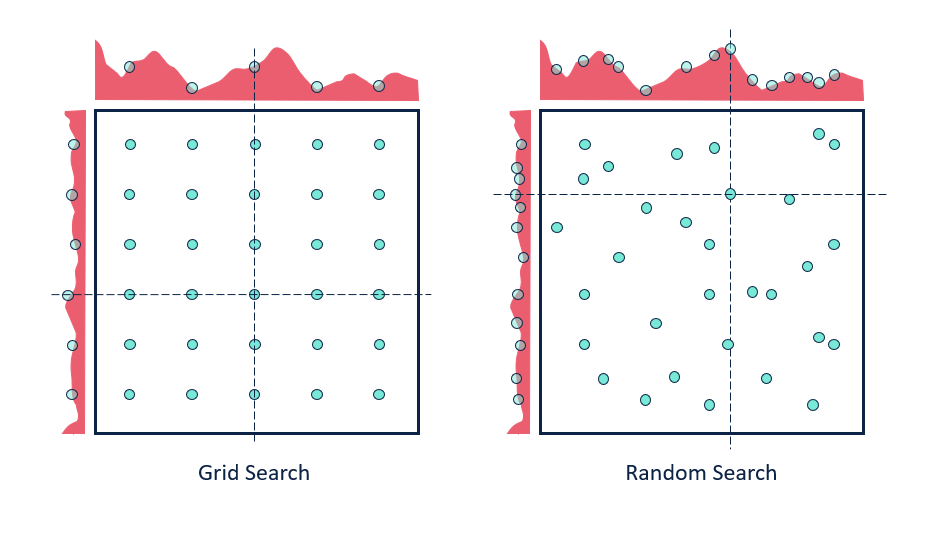
Una vez hemos elegido unos buenos valores iniciales, tenemos que empezar a explorar el espacio de hyperparámetros de nuestro problema para escoger la mejor combinación. Para ello tenemos dos opciones: grid search o random search. En el primer caso, definiremos todas las posibles combinaciones que queremos probar y las probaremos todas. Como puedes imaginar esto puede ser muy costoso y potencialmente ineficiente. La segunda opción es más recomendada, y consiste en definir un espacio de búsqueda y ejecutar un número determinado de entrenamientos, para cada cual escogeremos un conjunto de hiperparámetros aleatorios del espacio de búsqueda.

# ejemplo de random search

bss = [16, 32, 64, 128, 256]
lrs = [0.01, 0.005, 0.001, 0.0003, 0.0001]
n = 5
hists = []
for i in range(n):
    lr = random.choice(lrs)
    bs = random.choice(bss)
    print(f"Test {i+1} lr {lr} bs {bs}")
    dataloader = {
        'train': torch.utils.data.DataLoader(dataset['train'], batch_size=bs, shuffle=True),
        'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
    }
    model = build_model()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    hist = fit(model, dataloader, optimizer, epochs=20, verbose=0)
    hists.append({'hist': hist, 'lr': lr, 'bs': bs})

Test 1 lr 0.0001 bs 16
Test 2 lr 0.005 bs 32
Test 3 lr 0.01 bs 128
Test 4 lr 0.001 bs 256
Test 5 lr 0.0003 bs 16

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(121)
for i in range(len(hists)):
    ax.plot(hists[i]['hist']['loss'], label=f'lr {hists[i]["lr"]} bs {hists[i]["bs"]}')
ax.legend()
ax.grid(True)
ax.set_xlabel('epoch')
ax.set_ylabel('loss')
ax = plt.subplot(122)
for i in range(len(hists)):
    ax.plot(hists[i]['hist']['val_acc'], label=f'lr {hists[i]["lr"]} bs {hists[i]["bs"]}')
ax.legend()
ax.grid(True)
ax.set_ylabel('acc')
ax.set_xlabel('epoch')
plt.show()

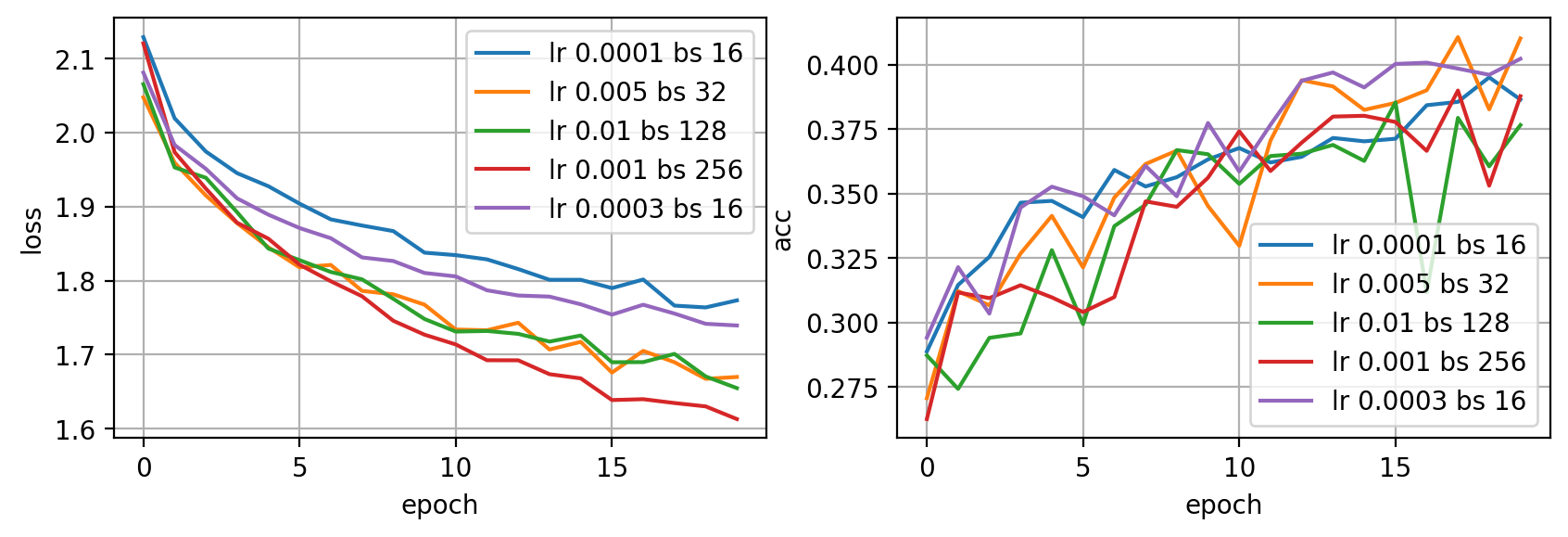
Últimos toques

Y ya para terminar, puedes experimentar con varios schedulers que vayan modificando el learning rate durante el entrenamiento. Esta técnica es especialmente interesante en combinación con transfer learning, algo de lo que hablaremos en detalle más adelante.

model = build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 20, 0.1)
hist = fit(model, dataloader, optimizer, scheduler, epochs=100, early_stopping=10, verbose=2)

Mejor modelo guardado con acc 0.31080 en epoch 1
Epoch 1/100 loss 2.05489 acc 0.25831 val_loss 1.94514 val_acc 0.31080 lr 0.00100
Mejor modelo guardado con acc 0.32250 en epoch 2
Epoch 2/100 loss 1.93188 acc 0.30578 val_loss 1.90078 val_acc 0.32250 lr 0.00100
Mejor modelo guardado con acc 0.33670 en epoch 3
Epoch 3/100 loss 1.89301 acc 0.31685 val_loss 1.83507 val_acc 0.33670 lr 0.00100
Mejor modelo guardado con acc 0.34370 en epoch 4
Epoch 4/100 loss 1.84616 acc 0.32615 val_loss 1.83057 val_acc 0.34370 lr 0.00100
Mejor modelo guardado con acc 0.35070 en epoch 5
Epoch 5/100 loss 1.80578 acc 0.35245 val_loss 1.79601 val_acc 0.35070 lr 0.00100
Mejor modelo guardado con acc 0.35320 en epoch 6
Epoch 6/100 loss 1.79223 acc 0.35225 val_loss 1.83164 val_acc 0.35320 lr 0.00100
Mejor modelo guardado con acc 0.35920 en epoch 7
Epoch 7/100 loss 1.77872 acc 0.36036 val_loss 1.80089 val_acc 0.35920 lr 0.00100
Mejor modelo guardado con acc 0.37300 en epoch 8
Epoch 8/100 loss 1.74652 acc 0.37025 val_loss 1.77220 val_acc 0.37300 lr 0.00100
Epoch 9/100 loss 1.73483 acc 0.37045 val_loss 1.83465 val_acc 0.34820 lr 0.00100
Epoch 10/100 loss 1.72215 acc 0.37856 val_loss 1.75865 val_acc 0.36260 lr 0.00100
Epoch 11/100 loss 1.71169 acc 0.38291 val_loss 1.83641 val_acc 0.36440 lr 0.00100
Mejor modelo guardado con acc 0.37450 en epoch 12
Epoch 12/100 loss 1.70279 acc 0.39221 val_loss 1.73932 val_acc 0.37450 lr 0.00100
Mejor modelo guardado con acc 0.37940 en epoch 13
Epoch 13/100 loss 1.69822 acc 0.38865 val_loss 1.73053 val_acc 0.37940 lr 0.00100
Mejor modelo guardado con acc 0.38040 en epoch 14
Epoch 14/100 loss 1.66658 acc 0.39478 val_loss 1.73423 val_acc 0.38040 lr 0.00100
Epoch 15/100 loss 1.67435 acc 0.39616 val_loss 1.78441 val_acc 0.36910 lr 0.00100
Mejor modelo guardado con acc 0.39760 en epoch 16
Epoch 16/100 loss 1.68357 acc 0.38588 val_loss 1.68814 val_acc 0.39760 lr 0.00100
Epoch 17/100 loss 1.65953 acc 0.39775 val_loss 1.70791 val_acc 0.39380 lr 0.00100
Epoch 18/100 loss 1.63580 acc 0.41021 val_loss 1.74490 val_acc 0.38470 lr 0.00100
Epoch 19/100 loss 1.64745 acc 0.40348 val_loss 1.70227 val_acc 0.39720 lr 0.00100
Epoch 20/100 loss 1.64419 acc 0.40071 val_loss 1.73934 val_acc 0.39030 lr 0.00100
Mejor modelo guardado con acc 0.41800 en epoch 21
Epoch 21/100 loss 1.60001 acc 0.41950 val_loss 1.62077 val_acc 0.41800 lr 0.00010
Mejor modelo guardado con acc 0.42330 en epoch 22
Epoch 22/100 loss 1.58566 acc 0.43493 val_loss 1.61723 val_acc 0.42330 lr 0.00010
Mejor modelo guardado con acc 0.43190 en epoch 23
Epoch 23/100 loss 1.57847 acc 0.43691 val_loss 1.60338 val_acc 0.43190 lr 0.00010
Mejor modelo guardado con acc 0.43730 en epoch 24
Epoch 24/100 loss 1.56727 acc 0.43256 val_loss 1.59904 val_acc 0.43730 lr 0.00010
Epoch 25/100 loss 1.57552 acc 0.43968 val_loss 1.61462 val_acc 0.42870 lr 0.00010
Epoch 26/100 loss 1.57722 acc 0.43987 val_loss 1.61305 val_acc 0.43120 lr 0.00010
Epoch 27/100 loss 1.56216 acc 0.43710 val_loss 1.59914 val_acc 0.43260 lr 0.00010
Epoch 28/100 loss 1.57086 acc 0.43770 val_loss 1.60749 val_acc 0.42780 lr 0.00010
Epoch 29/100 loss 1.56997 acc 0.43058 val_loss 1.60015 val_acc 0.43470 lr 0.00010
Epoch 30/100 loss 1.56233 acc 0.44581 val_loss 1.61287 val_acc 0.42940 lr 0.00010
Epoch 31/100 loss 1.55527 acc 0.44600 val_loss 1.60850 val_acc 0.43370 lr 0.00010
Epoch 32/100 loss 1.54778 acc 0.44462 val_loss 1.61011 val_acc 0.43190 lr 0.00010
Epoch 33/100 loss 1.56426 acc 0.43493 val_loss 1.61146 val_acc 0.43140 lr 0.00010
Entrenamiento detenido en epoch 34 por no mejorar en 10 epochs seguidas

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(131)
pd.DataFrame(hist).plot(x='epoch', y=['loss', 'val_loss'], grid=True, ax=ax)
ax = plt.subplot(132)
pd.DataFrame(hist).plot(x='epoch', y=['acc', 'val_acc'], grid=True, ax=ax)
ax = plt.subplot(133)
pd.DataFrame(hist).plot(x='epoch', y=['lr'], grid=True, ax=ax)
plt.tight_layout()
plt.show()

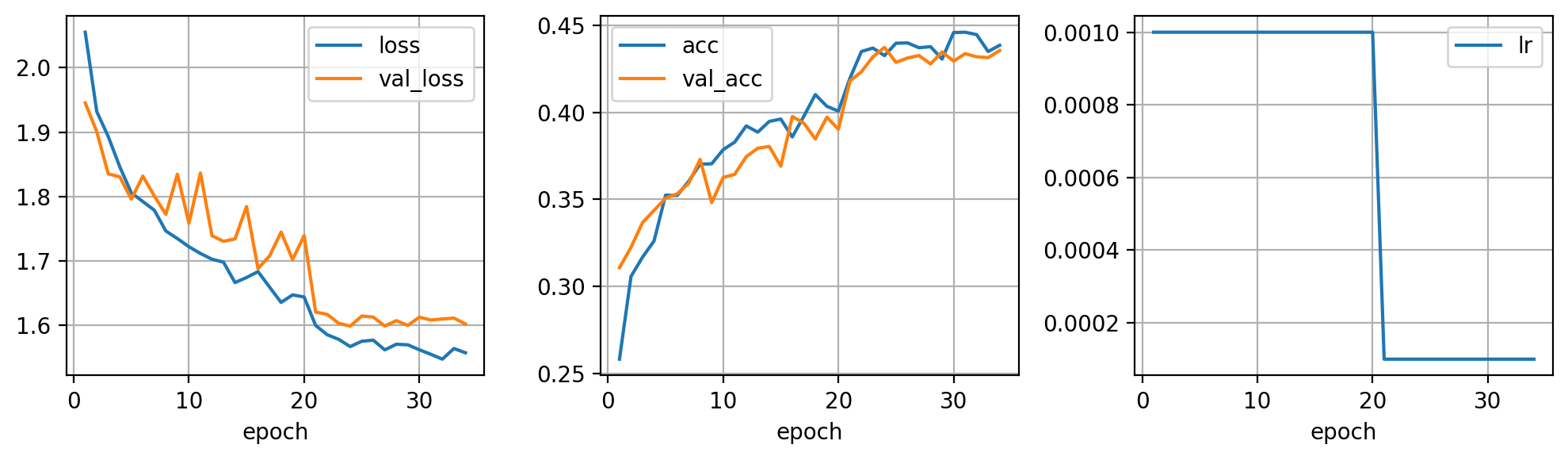
Y, por supuesto, utilizar todos los datos una vez hayas encontrado una buena combinación de hyperparámetros en tu subset.

dataset = {
    'train': Dataset(X_train, y_train, trans=trans),
    'val': Dataset(X_val, y_val),
}

dataloader = {
    'train': torch.utils.data.DataLoader(dataset['train'], batch_size=64, shuffle=True),
    'val': torch.utils.data.DataLoader(dataset['val'], batch_size=1000, shuffle=False)
}

len(dataset['train']), len(dataset['val'])

(40000, 10000)

model = build_model()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 20, 0.1)
hist = fit(model, dataloader, optimizer, scheduler, epochs=100, early_stopping=10, verbose=2)

Mejor modelo guardado con acc 0.33990 en epoch 1
Epoch 1/100 loss 1.88322 acc 0.31712 val_loss 1.79590 val_acc 0.33990 lr 0.00100
Epoch 2/100 loss 1.74840 acc 0.36907 val_loss 1.82805 val_acc 0.32530 lr 0.00100
Mejor modelo guardado con acc 0.40610 en epoch 3
Epoch 3/100 loss 1.69133 acc 0.39232 val_loss 1.65002 val_acc 0.40610 lr 0.00100
Epoch 4/100 loss 1.66370 acc 0.40090 val_loss 1.69876 val_acc 0.37730 lr 0.00100
Mejor modelo guardado con acc 0.43050 en epoch 5
Epoch 5/100 loss 1.63808 acc 0.41415 val_loss 1.58901 val_acc 0.43050 lr 0.00100
Mejor modelo guardado con acc 0.44030 en epoch 6
Epoch 6/100 loss 1.61763 acc 0.41565 val_loss 1.56114 val_acc 0.44030 lr 0.00100
Mejor modelo guardado con acc 0.44460 en epoch 7
Epoch 7/100 loss 1.60659 acc 0.42140 val_loss 1.55860 val_acc 0.44460 lr 0.00100
Mejor modelo guardado con acc 0.44810 en epoch 8
Epoch 8/100 loss 1.58716 acc 0.42983 val_loss 1.54961 val_acc 0.44810 lr 0.00100
Epoch 9/100 loss 1.58406 acc 0.43030 val_loss 1.54121 val_acc 0.44510 lr 0.00100
Mejor modelo guardado con acc 0.44980 en epoch 10
Epoch 10/100 loss 1.57007 acc 0.43490 val_loss 1.53185 val_acc 0.44980 lr 0.00100
Epoch 11/100 loss 1.56779 acc 0.43743 val_loss 1.54593 val_acc 0.44530 lr 0.00100
Mejor modelo guardado con acc 0.46330 en epoch 12
Epoch 12/100 loss 1.55756 acc 0.43928 val_loss 1.49551 val_acc 0.46330 lr 0.00100
Epoch 13/100 loss 1.54649 acc 0.44538 val_loss 1.50299 val_acc 0.46310 lr 0.00100
Epoch 14/100 loss 1.54381 acc 0.44255 val_loss 1.50358 val_acc 0.45810 lr 0.00100
Mejor modelo guardado con acc 0.47010 en epoch 15
Epoch 15/100 loss 1.53651 acc 0.44810 val_loss 1.48716 val_acc 0.47010 lr 0.00100
Mejor modelo guardado con acc 0.47810 en epoch 16
Epoch 16/100 loss 1.52789 acc 0.45165 val_loss 1.45735 val_acc 0.47810 lr 0.00100
Epoch 17/100 loss 1.52592 acc 0.45160 val_loss 1.46789 val_acc 0.47550 lr 0.00100
Mejor modelo guardado con acc 0.47850 en epoch 18
Epoch 18/100 loss 1.51266 acc 0.45427 val_loss 1.46614 val_acc 0.47850 lr 0.00100
Epoch 19/100 loss 1.51064 acc 0.45285 val_loss 1.47450 val_acc 0.46780 lr 0.00100
Mejor modelo guardado con acc 0.48350 en epoch 20
Epoch 20/100 loss 1.50256 acc 0.46285 val_loss 1.45791 val_acc 0.48350 lr 0.00100
Mejor modelo guardado con acc 0.50100 en epoch 21
Epoch 21/100 loss 1.48207 acc 0.46950 val_loss 1.39730 val_acc 0.50100 lr 0.00010
Mejor modelo guardado con acc 0.50140 en epoch 22
Epoch 22/100 loss 1.46167 acc 0.47568 val_loss 1.39544 val_acc 0.50140 lr 0.00010
Epoch 23/100 loss 1.46038 acc 0.47723 val_loss 1.39221 val_acc 0.50050 lr 0.00010
Epoch 24/100 loss 1.46276 acc 0.47550 val_loss 1.39816 val_acc 0.50030 lr 0.00010
Epoch 25/100 loss 1.45494 acc 0.47930 val_loss 1.39653 val_acc 0.49830 lr 0.00010
Epoch 26/100 loss 1.45062 acc 0.48283 val_loss 1.38615 val_acc 0.50060 lr 0.00010
Epoch 27/100 loss 1.45784 acc 0.47920 val_loss 1.38790 val_acc 0.50030 lr 0.00010
Mejor modelo guardado con acc 0.50330 en epoch 28
Epoch 28/100 loss 1.44891 acc 0.48083 val_loss 1.38020 val_acc 0.50330 lr 0.00010
Epoch 29/100 loss 1.43959 acc 0.48607 val_loss 1.38246 val_acc 0.50210 lr 0.00010
Mejor modelo guardado con acc 0.50620 en epoch 30
Epoch 30/100 loss 1.44894 acc 0.48307 val_loss 1.38263 val_acc 0.50620 lr 0.00010
Epoch 31/100 loss 1.44708 acc 0.47957 val_loss 1.38679 val_acc 0.50190 lr 0.00010
Epoch 32/100 loss 1.44216 acc 0.48330 val_loss 1.38015 val_acc 0.50550 lr 0.00010
Mejor modelo guardado con acc 0.50640 en epoch 33
Epoch 33/100 loss 1.44292 acc 0.48480 val_loss 1.38072 val_acc 0.50640 lr 0.00010
Epoch 34/100 loss 1.45016 acc 0.48157 val_loss 1.38227 val_acc 0.50150 lr 0.00010
Epoch 35/100 loss 1.43801 acc 0.48597 val_loss 1.38157 val_acc 0.50620 lr 0.00010
Epoch 36/100 loss 1.44160 acc 0.48468 val_loss 1.38085 val_acc 0.50530 lr 0.00010
Epoch 37/100 loss 1.43691 acc 0.48607 val_loss 1.38479 val_acc 0.50620 lr 0.00010
Mejor modelo guardado con acc 0.50660 en epoch 38
Epoch 38/100 loss 1.43930 acc 0.48413 val_loss 1.37357 val_acc 0.50660 lr 0.00010
Mejor modelo guardado con acc 0.50970 en epoch 39
Epoch 39/100 loss 1.43706 acc 0.48552 val_loss 1.37579 val_acc 0.50970 lr 0.00010
Epoch 40/100 loss 1.44572 acc 0.48407 val_loss 1.37282 val_acc 0.50780 lr 0.00010
Epoch 41/100 loss 1.43833 acc 0.48255 val_loss 1.37641 val_acc 0.50560 lr 0.00001
Epoch 42/100 loss 1.43483 acc 0.48740 val_loss 1.37409 val_acc 0.50630 lr 0.00001
Epoch 43/100 loss 1.43363 acc 0.48628 val_loss 1.38017 val_acc 0.50730 lr 0.00001
Epoch 44/100 loss 1.42896 acc 0.48997 val_loss 1.37709 val_acc 0.50670 lr 0.00001
Epoch 45/100 loss 1.43057 acc 0.48688 val_loss 1.37971 val_acc 0.50590 lr 0.00001
Epoch 46/100 loss 1.43220 acc 0.48605 val_loss 1.37531 val_acc 0.50830 lr 0.00001
Mejor modelo guardado con acc 0.51150 en epoch 47
Epoch 47/100 loss 1.42635 acc 0.48815 val_loss 1.37129 val_acc 0.51150 lr 0.00001
Epoch 48/100 loss 1.43484 acc 0.48623 val_loss 1.37681 val_acc 0.50550 lr 0.00001
Epoch 49/100 loss 1.43807 acc 0.48707 val_loss 1.37004 val_acc 0.50940 lr 0.00001
Epoch 50/100 loss 1.42954 acc 0.48933 val_loss 1.37751 val_acc 0.50780 lr 0.00001
Epoch 51/100 loss 1.43486 acc 0.48700 val_loss 1.37292 val_acc 0.50750 lr 0.00001
Epoch 52/100 loss 1.43457 acc 0.48855 val_loss 1.36988 val_acc 0.51090 lr 0.00001
Epoch 53/100 loss 1.43915 acc 0.48523 val_loss 1.37393 val_acc 0.50880 lr 0.00001
Mejor modelo guardado con acc 0.51190 en epoch 54
Epoch 54/100 loss 1.43597 acc 0.48797 val_loss 1.37116 val_acc 0.51190 lr 0.00001
Epoch 55/100 loss 1.42729 acc 0.48745 val_loss 1.36892 val_acc 0.51020 lr 0.00001
Epoch 56/100 loss 1.42994 acc 0.49020 val_loss 1.37152 val_acc 0.50890 lr 0.00001
Epoch 57/100 loss 1.43192 acc 0.48660 val_loss 1.37178 val_acc 0.50920 lr 0.00001
Epoch 58/100 loss 1.42799 acc 0.48665 val_loss 1.37249 val_acc 0.50980 lr 0.00001
Epoch 59/100 loss 1.43478 acc 0.48550 val_loss 1.37385 val_acc 0.50770 lr 0.00001
Epoch 60/100 loss 1.43087 acc 0.48785 val_loss 1.36637 val_acc 0.51190 lr 0.00001
Epoch 61/100 loss 1.42932 acc 0.48783 val_loss 1.37310 val_acc 0.50990 lr 0.00000
Epoch 62/100 loss 1.43183 acc 0.48605 val_loss 1.37069 val_acc 0.51180 lr 0.00000
Epoch 63/100 loss 1.43087 acc 0.48930 val_loss 1.37216 val_acc 0.50780 lr 0.00000
Entrenamiento detenido en epoch 64 por no mejorar en 10 epochs seguidas

fig = plt.figure(dpi=200, figsize=(10,3))
ax = plt.subplot(131)
pd.DataFrame(hist).plot(x='epoch', y=['loss', 'val_loss'], grid=True, ax=ax)
ax = plt.subplot(132)
pd.DataFrame(hist).plot(x='epoch', y=['acc', 'val_acc'], grid=True, ax=ax)
ax = plt.subplot(133)
pd.DataFrame(hist).plot(x='epoch', y=['lr'], grid=True, ax=ax)
plt.tight_layout()
plt.show()

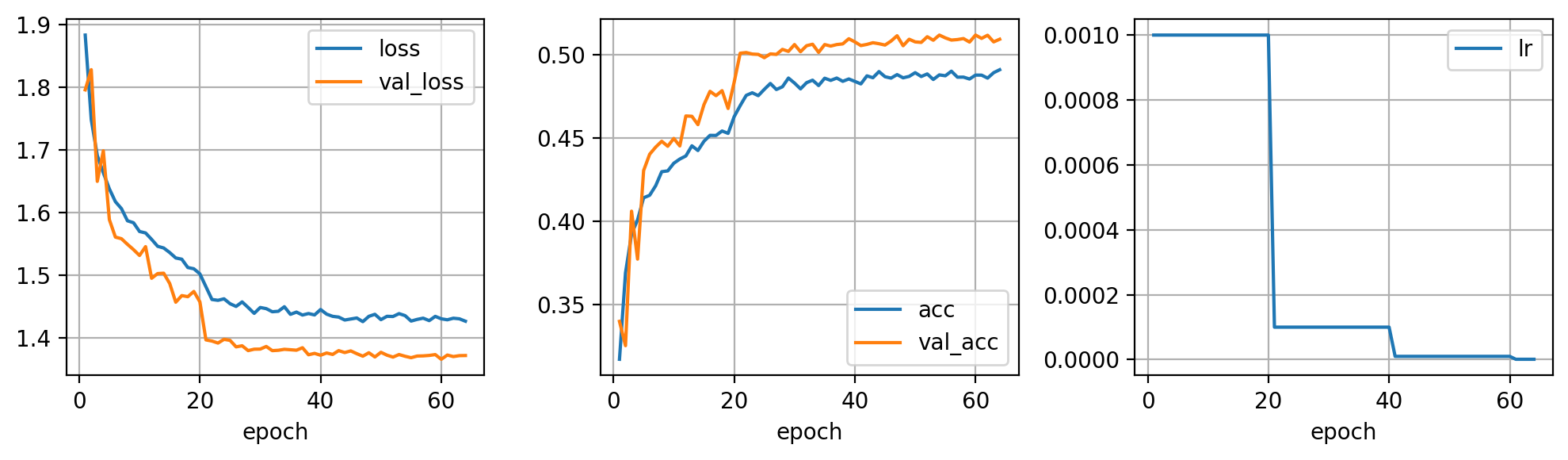
Resumen

En este post hemos presentado una "receta" para entrenar redes neuronales de manera efectiva. Siguiendo estos pasos podrás diseñar tus arquitecturas, validar que sean correctas haciendo fit primero de una sola muestra, luego de un batch y por último utilizando un pequeño conjunto de datos para encontrar de manera rápida una combinación óptima de hyperparámetros a partir de una configuración recomendad con valores iniciales que suelen funcionar bien en la práctica. A partir de aquí, podrás mejorar tu modelo con técnicas más sofisticadas que te darán un extra en la performance de tus modelos.