septiembre 25, 2020
~ 14 MIN
Implementando SSD
< Blog RSSImplementando SSD
En este post vamos a implementar una red neuronal convolucional para detección de objetos desde cero. Para ello nos inspiramos en el modelo SSD, una arquitectura muy utilizada por su versatilidad y eficiencia.
import torch
import torchvision
device = "cuda" if torch.cuda.is_available() else "cpu"
device
'cpu'
Vamos a utilizar el mismo dataset que conocemos de posts anteriores, el dataset VOC.
train = torchvision.datasets.VOCDetection('./data', download=True)
len(train)
Using downloaded and verified file: ./data/VOCtrainval_11-May-2012.tar
5717
classes = ["background","aeroplane","bicycle","bird","boat",
"bottle","bus","car","cat","chair","cow","diningtable","dog",
"horse","motorbike","person","pottedplant","sheep","sofa",
"train","tvmonitor"]
Las siguientes funciones nos ayudan a extraer la información que necesitamos de las anotaciones y a visualizar muestras del dataset.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.patheffects as PathEffects
import random
def get_sample(ix):
img, label = train[ix]
img_np = np.array(img)
anns = label['annotation']['object']
if type(anns) is not list:
anns = [anns]
labels = np.array([classes.index(ann['name']) for ann in anns])
bbs = [ann['bndbox'] for ann in anns]
bbs = np.array([[int(bb['xmin']), int(bb['ymin']),int(bb['xmax']),int(bb['ymax'])] for bb in bbs])
anns = (labels, bbs)
return img_np, anns
def plot_anns(img, anns, ax=None, bg=-1):
# anns is a tuple with (labels, bbs)
# bbs is an array of bounding boxes in format [x_min, y_min, x_max, y_max]
# labels is an array containing the label
if not ax:
fig, ax = plt.subplots(figsize=(10, 6))
ax.imshow(img)
labels, bbs = anns
for lab, bb in zip(labels, bbs):
if bg == -1 or lab != bg:
x, y, xm, ym = bb
w, h = xm - x, ym - y
rect = mpatches.Rectangle((x, y), w, h, fill=False, edgecolor='red', linewidth=2)
text = ax.text(x, y - 10, classes[lab], {'color': 'red'})
text.set_path_effects([PathEffects.withStroke(linewidth=5, foreground='w')])
ax.add_patch(rect)
r, c = 3, 4
fig = plt.figure(figsize=(4*c, 4*r))
for _r in range(r):
for _c in range(c):
ax = plt.subplot(r, c, _r*c + _c + 1)
ix = random.randint(0, len(train)-1)
ax.set_title(ix)
img_np, anns = get_sample(ix)
plot_anns(img_np, anns, ax)
plt.axis("off")
plt.tight_layout()
plt.show()

Como puedes ver, en el dataset hay imágenes con una detección, otras con más de una. Algunas detecciones ocupan gran parte de la imagen, otras son pequeñas. En algunas imágenes incluso podemos tener múltiples detecciones de la misma clase... ¿Cómo podemos definir un modelo que sea capaz de darnos un número indeterminado de detecciones? En el caso del modelo SSD, y en general todos los detectores de una etapa, nosotros definimos un conjunto de cajas definido que la red utilizará durante el entrenamiento para generar detecciones.
Propuesta de cajas
def norm(bb, shape):
# normalize bb
# shape = (heigh, width)
# bb = [x_min, y_min, x_max, y_max]
h, w = shape
return np.array([bb[0]/w, bb[1]/h, bb[2]/w, bb[3]/h])
def unnorm(bb, shape):
# unnormalize bb
# shape = (heigh, width)
# bb = [x_min, y_min, x_max, y_max]
h, w = shape
return np.array([bb[0]*w, bb[1]*h, bb[2]*w, bb[3]*h])
def xyxy2xywh(bb):
return torch.stack([bb[:,0], bb[:,1], bb[:,2]-bb[:,0], bb[:,3]-bb[:,1]], axis=1)
#def xywh2xyxy(bb):
# return torch.stack([bb[:,0], bb[:,1], bb[:,0]+bb[:,2], bb[:,1]+bb[:,3]], axis=1)
def generate_anchors(scales, centers, sizes):
k, anchors, grid_size = [], [], []
for s in scales:
cnt = 0
for (x, y) in centers:
for (w, h) in sizes:
for i in range(s):
for j in range(s):
# cwh
#anchors.append(np.array([x+i, y+j, w, h])/s)
# xyxy
anchors.append(np.array([x+i-w/2, y+j-h/2, x+i+w/2, y+j+h/2])/s)
grid_size.append(np.array([1./s,1./s]))
cnt = cnt + 1
k.append(cnt)
return k, torch.tensor(anchors).float(), torch.tensor(grid_size).float()
A la función generate_anchors le damos una lista de diferentes escalas a las cuales queremos tener detecciones, otra con el centro de las cajas, la escala y el aspect ratio. La función nos devuelve una lista con todas las cajas que el modelo tendrá en cuenta durante el entrenamiento para detectar objetos en ellas.
def plot_anchors(img, anns, anchors, ax=None, overlap=False):
# anns is a tuple with (bbs, labels)
# bbs is an array of bounding boxes in format [x_min, y_min, x_max, y_max]
# labels is an array containing the label
if not ax:
fig, ax = plt.subplots(figsize=(10, 6))
ax.imshow(img)
labels, bbs = anns
anchors = xyxy2xywh(anchors)
_anchors = np.array([unnorm(a, img.shape[:2]) for a in anchors])
for a in _anchors:
x, y, w, h = a
rect = mpatches.Rectangle((x, y), w, h, fill=False, edgecolor='green', linewidth=2)
ax.add_patch(rect)
labels, bbs = anns
for lab, bb in zip(labels, bbs):
x, y, xm, ym = bb
w, h = xm - x, ym - y
rect = mpatches.Rectangle((x, y), w, h, fill=False, edgecolor='red', linewidth=2)
text = ax.text(x, y - 10, classes[lab], {'color': 'red'})
text.set_path_effects([PathEffects.withStroke(linewidth=5, foreground='w')])
ax.add_patch(rect)
ix = 4445
img_np, anns = get_sample(ix)
labels, bbs = anns
scales = [6, 3, 1]
centers = [(0.5, 0.5)]
size_scales = [0.5]
aspect_ratios = [(1., 1.), (1.5, 0.8), (1.8, 0.4)]
sizes = [(s*a[0], s*a[1]) for s in size_scales for a in aspect_ratios]
k, anchors, grid_size = generate_anchors(scales, centers, sizes)
plot_anchors(img_np, anns, anchors)
len(anchors), k
(138, [3, 3, 3])
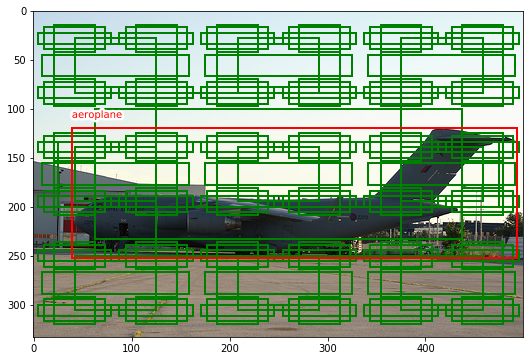
La eficiencia y precisión del modelo dependerá del número de cajas que propongamos así como su número. Muchas cajas nos darán un modelo lento, pero potencialmente más preciso. Por otro lado, si en nuestra aplicación conocemos bien la escala y tamaño al que se encuentran los objetos que queremos detectar, poner sólo cajas en esas escalas dará como resultado un modelo preciso y eficiente (aquí estaremos introduciendo conocimiento experto, o priors, a nuestro modelo perdiendo flexibilidad).
Como puedes estar pensando, de querer ser capaces de detectar objetos de manera precisa simplemente con las cajas propuestas, deberíamos tener muchísimas de estas cajas (potencialmente cubriendo todo el espacio). Es por esto que nuestro modelo no sólo clasificará objetos dentro de las cajas propuestas sino que además también predecirá unos offsets, modificaciones sobre las cajas propuestas, para acabar de ajustar la detección (básicamente, un offset en el centro de la caja, su ancho y alto).
El Modelo
Inspirándonos en la implementación del modelo SSD original, necesitamos una backbone que extraiga características de la imagen y luego varias heads que produzcan las clasificaciones y los offests sobre las cajas propuestas. Estas heads son alimentadas con las salidas de diferentes capas convolucionales de la backbone, permitiendo así la detección a múltiples escalas. Estas escalas deben coincidir con las definidas a la hora de generar nuestras propuestas de cajas (si no las dimensiones no encajarán).

def block(c_in, c_out, k=3, p=1, s=1, pk=2, ps=2):
return torch.nn.Sequential(
torch.nn.Conv2d(c_in, c_out, k, padding=p, stride=s),
torch.nn.ReLU(),
#torch.nn.BatchNorm2d(c_out),
torch.nn.MaxPool2d(pk, stride=ps)
)
def flatten_conv(x, k):
return x.view(x.size(0), x.size(1)//k, -1).transpose(1,2)
class out_conv(torch.nn.Module):
def __init__(self, c_in, k, n_classes):
super().__init__()
self.k = k
self.oconv1 = torch.nn.Conv2d(c_in, k*4, 3, padding=1)
self.oconv2 = torch.nn.Conv2d(c_in, k*n_classes, 3, padding=1)
def forward(self, x):
return [
flatten_conv(self.oconv1(x), self.k),
flatten_conv(self.oconv2(x), self.k)
]
def conv(c_i, c_o, stride=2, padding=1):
return nn.Sequential(
nn.Conv2d(c_i, c_o, 3, stride=stride, padding=padding),
nn.ReLU(),
#nn.BatchNorm2d(c_o)
)
class SSD(torch.nn.Module):
def __init__(self, n_channels=3, n_classes=20, k=[1, 1, 1]):
super().__init__()
# backbone
self.conv1 = block(n_channels, 8)
self.conv2 = block(8, 16)
self.conv3 = block(16, 32)
self.conv4 = block(32, 64)
self.conv5 = block(64, 64)
self.conv6 = block(64, 64)
# head
self.k = k
self.out4 = out_conv(64, self.k[0], n_classes)
self.out5 = out_conv(64, self.k[1], n_classes)
self.out6 = out_conv(64, self.k[2], n_classes)
def forward(self, x):
# backbone
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x) # para inputs de 100x100
x4 = self.conv4(x) # 6x6
x5 = self.conv5(x4) # 3x3
x6 = self.conv6(x5) # 1x1
# head
o1l, o1c = self.out4(x4)
o2l, o2c = self.out5(x5)
o3l, o3c = self.out6(x6)
return torch.cat([o1l,o2l,o3l],dim=1), torch.cat([o1c,o2c,o3c],dim=1)
#return o2l, o2c
net = SSD(n_classes=len(classes), k=k)
output = net(torch.rand((64,3,100,100)))
output[0].shape, output[1].shape
(torch.Size([64, 138, 4]), torch.Size([64, 138, 21]))
La función de pérdida
Durante el entrenamiento, el modelo nos dará 4 valores para cada una de las cajas propuestas (offests) así como las 21 probabilidades asignadas a cada clase. De alguna manera, la función de pérdida tiene que comparar estos valores con las cajas reales. En primer lugar tenemos que coger las salidas del modelo y calcular los offsets. Para ello, usaremos la función tanh, que limita los salidas a valores en el rango (-1, 1), permitiendo un offset de hasta el 50% del tamaños de la caja en ambas dimensiones.
def actn_to_bb(actn, anchors, grid_size):
actn_bbs = torch.tanh(actn)
actn_p1 = anchors[:,:2] + actn_bbs[:,:2]*grid_size*0.5
actn_p2 = anchors[:,2:] + actn_bbs[:,2:]*grid_size*0.5
return torch.cat([actn_p1, actn_p2], dim=1)
El siguiente problema es que cada imagen tiene un número indeterminado de detecciones, por lo que primero tenemos que emparejar las cajas propuestas con aquellas anotaciones con las que mejor coincidan. Para ello usamos una métrica conocida como IoU(intersection over unions).
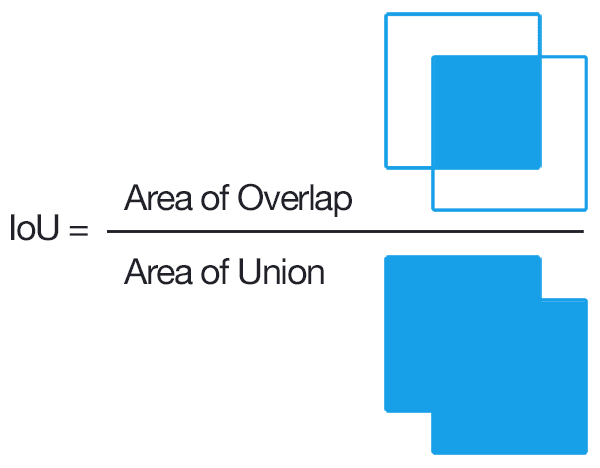
Una vez calculado este valor para cada caja propuesta con respecto a todas las cajas en las etiquetas, nos quedamos con aquellas que superen un threshold determinado (por defecto 0.4). Es posible pues tener varias detecciones para un mismo objeto, algo que resolveremos más adelante. También puede ocurrir que no haya ninguna caja que cumpla estos requisitos, es este caso le asignaremos aquella con mayor IoU.
def map_to_ground_truth(overlaps):
prior_overlap, prior_idx = overlaps.max(1)
gt_overlap, gt_idx = overlaps.max(0)
gt_overlap[prior_idx] = 1.99
for i,o in enumerate(prior_idx): gt_idx[o] = i
return gt_overlap, gt_idx
Una vez hemos determinado las cajas que mejor aproximan las detecciones reales, usamos una combinación de L1Loss y CrossEntropyLoss para la localización y clasificación, respectivamente, igual que hicimos en este post.
class SSDLoss(torch.nn.Module):
def __init__(self, anchors, grid_size, threshold=0.4):
super().__init__()
self.loc_loss = torch.nn.L1Loss()
self.class_loss = torch.nn.CrossEntropyLoss()
self.anchors = anchors.to(device)
self.grid_size = grid_size.to(device)
self.threshold = threshold
def forward(self, preds, target):
pred_bbs, pred_cs = preds
tar_bbs, c_t = target # B x O x 4, B x O
# cada imagen del batch puede tener un número diferente de detecciones
loc_loss, clas_loss = 0, 0
for pred_bb, pred_c, tar_bb, tar_c in zip(pred_bbs, pred_cs, tar_bbs, c_t):
labels = torch.zeros(len(self.anchors)).long() # por defecto todas las etiquetas son `background`
if tar_bb.shape[0] is not 0: # es posible que haya imágenes sin detecciones
# calculamos el IoU de las detecciones con las cajas
overlaps = torchvision.ops.box_iou(tar_bb, self.anchors)
# nos quedamos con aquellas que coincidan
gt_overlap, gt_idx = map_to_ground_truth(overlaps)
pos = gt_overlap > self.threshold
# optimizamos para aquellas cajas que superen el filtro
pos_idx = torch.nonzero(pos)[:,0]
tar_idx = gt_idx[pos_idx]
pred_bb = actn_to_bb(pred_bb, self.anchors, self.grid_size)
_anchors = pred_bb[pos_idx]
tar_bb = tar_bb[tar_idx]
loc_loss += self.loc_loss(_anchors, tar_bb)
labels[pos_idx] = tar_c[tar_idx]
clas_loss += self.class_loss(pred_c, labels)
return clas_loss + loc_loss
Entrenamiento
Ahora ya tenemos todas las piezas en sus sitio para entrenar nuestro modelo. Vamos a hacer el fit de una sola imagen para simplificar las cosas de momento.
def fit(model, X, target, epochs=1, lr=3e-4):
model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = SSDLoss(anchors, grid_size)
for epoch in range(1, epochs+1):
model.train()
train_loss_loc, train_loss_cls = [], []
optimizer.zero_grad()
outputs = model(X)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
train_loss_loc.append(loss.item())
print(f"Epoch {epoch}/{epochs} loss {np.mean(train_loss_loc):.5f}")
Hemos diseñado nuestra red y nuestras cajas propuestas para trabajar con imágenes de 100 x 100 pixeles. Utilizamos albumentations para hacer el resize de la imagen y anotaciones.
import albumentations as A
trans = A.Compose([
A.Resize(100, 100)
], bbox_params=A.BboxParams(format='pascal_voc', label_fields=['labels']))
labels, bbs = anns
augmented = trans(**{'image': img_np, 'bboxes': bbs, 'labels': labels})
img, bbs, labels = augmented['image'], augmented['bboxes'], augmented['labels']
plot_anchors(img, (labels, bbs), anchors)
plt.show()

img_tensor = torch.FloatTensor(img / 255.).permute(2,0,1).unsqueeze(0).to(device)
bb_norm = [norm(bb, img.shape[:2]) for bb in bbs]
bb_tensor = torch.FloatTensor(bb_norm).unsqueeze(0).to(device)
label_tensor = torch.tensor(labels).long().unsqueeze(0).to(device)
img_tensor.shape, bb_tensor.shape, label_tensor.shape
(torch.Size([1, 3, 100, 100]), torch.Size([1, 1, 4]), torch.Size([1, 1]))
model = SSD(n_classes = len(classes), k=k)
fit(model, img_tensor, (bb_tensor, label_tensor), epochs=100)
Epoch 1/100 loss 3.15287
Epoch 2/100 loss 3.14288
Epoch 3/100 loss 3.13321
Epoch 4/100 loss 3.12305
Epoch 5/100 loss 3.11200
Epoch 6/100 loss 3.09954
Epoch 7/100 loss 3.08533
Epoch 8/100 loss 3.06889
Epoch 9/100 loss 3.04957
Epoch 10/100 loss 3.02663
Epoch 11/100 loss 2.99950
Epoch 12/100 loss 2.96707
Epoch 13/100 loss 2.92832
Epoch 14/100 loss 2.88331
Epoch 15/100 loss 2.82919
Epoch 16/100 loss 2.76437
Epoch 17/100 loss 2.68728
Epoch 18/100 loss 2.59801
Epoch 19/100 loss 2.49365
Epoch 20/100 loss 2.37002
Epoch 21/100 loss 2.22362
Epoch 22/100 loss 2.05320
Epoch 23/100 loss 1.87045
Epoch 24/100 loss 1.66518
Epoch 25/100 loss 1.44438
Epoch 26/100 loss 1.22984
Epoch 27/100 loss 1.02189
Epoch 28/100 loss 0.83204
Epoch 29/100 loss 0.66695
Epoch 30/100 loss 0.52934
Epoch 31/100 loss 0.41900
Epoch 32/100 loss 0.33453
Epoch 33/100 loss 0.27127
Epoch 34/100 loss 0.22592
Epoch 35/100 loss 0.19698
Epoch 36/100 loss 0.17037
Epoch 37/100 loss 0.14681
Epoch 38/100 loss 0.13502
Epoch 39/100 loss 0.12954
Epoch 40/100 loss 0.12270
Epoch 41/100 loss 0.11753
Epoch 42/100 loss 0.10648
Epoch 43/100 loss 0.09597
Epoch 44/100 loss 0.08817
Epoch 45/100 loss 0.08916
Epoch 46/100 loss 0.08063
Epoch 47/100 loss 0.06748
Epoch 48/100 loss 0.05360
Epoch 49/100 loss 0.04503
Epoch 50/100 loss 0.04861
Epoch 51/100 loss 0.05203
Epoch 52/100 loss 0.04910
Epoch 53/100 loss 0.04707
Epoch 54/100 loss 0.04641
Epoch 55/100 loss 0.04243
Epoch 56/100 loss 0.03418
Epoch 57/100 loss 0.03255
Epoch 58/100 loss 0.03288
Epoch 59/100 loss 0.03527
Epoch 60/100 loss 0.02956
Epoch 61/100 loss 0.02656
Epoch 62/100 loss 0.02485
Epoch 63/100 loss 0.03326
Epoch 64/100 loss 0.03313
Epoch 65/100 loss 0.03171
Epoch 66/100 loss 0.02562
Epoch 67/100 loss 0.02153
Epoch 68/100 loss 0.02212
Epoch 69/100 loss 0.02372
Epoch 70/100 loss 0.02117
Epoch 71/100 loss 0.02024
Epoch 72/100 loss 0.02144
Epoch 73/100 loss 0.02175
Epoch 74/100 loss 0.02112
Epoch 75/100 loss 0.01938
Epoch 76/100 loss 0.01811
Epoch 77/100 loss 0.01649
Epoch 78/100 loss 0.01880
Epoch 79/100 loss 0.01674
Epoch 80/100 loss 0.01952
Epoch 81/100 loss 0.02427
Epoch 82/100 loss 0.02252
Epoch 83/100 loss 0.01553
Epoch 84/100 loss 0.01117
Epoch 85/100 loss 0.01250
Epoch 86/100 loss 0.01447
Epoch 87/100 loss 0.01354
Epoch 88/100 loss 0.01616
Epoch 89/100 loss 0.01428
Epoch 90/100 loss 0.01080
Epoch 91/100 loss 0.01234
Epoch 92/100 loss 0.01166
Epoch 93/100 loss 0.01102
Epoch 94/100 loss 0.00841
Epoch 95/100 loss 0.01047
Epoch 96/100 loss 0.01005
Epoch 97/100 loss 0.00986
Epoch 98/100 loss 0.01070
Epoch 99/100 loss 0.01092
Epoch 100/100 loss 0.00883
Generando predicciones
Una vez tenemos nuestro modelo entrenado, podemos generar predicciones de la siguiente manera
def predict(model, X):
model.eval()
with torch.no_grad():
X = X.to(device)
bbs, labels = model(X)
bbs = actn_to_bb(bbs[0].cpu(), anchors, grid_size)
return bbs, torch.max(torch.softmax(labels, axis=2)[0], axis=1)
bbs, (scores, labels) = predict(model, img_tensor)
bbs = [unnorm(bb, img.shape[:2]) for bb in bbs]
plot_anns(img, (labels, bbs))
plt.show()

Tenemos tantas predicciones como cajas propuestas, y la mayoría por defecto tendrán asignada la clase background que no nos interesa, así que descartamos todas estas cajas.
plot_anns(img, (labels, bbs), bg=0)
plt.show()

Aún así, es posible que tengamos varias detecciones para un mismo objeto. Para resolver este problema podemos aplicar el algoritmo NMS(non maximum supression) que calcula el IoU de las detecciones con la misma clase y, si este valor está por encima de un cierto threshold, devuelve solo la detección con mayor probabilidad.
bbs, (scores, labels) = predict(model, img_tensor)
# quitar bg
bbs, labels, scores = bbs[labels > 0], labels[labels > 0], scores[labels > 0]
bbs, labels, scores
(tensor([[0.0724, 0.3656, 0.9923, 0.7584],
[0.0864, 0.3451, 0.9954, 0.7547],
[0.0533, 0.3503, 0.9910, 0.7586]]),
tensor([1, 1, 1]),
tensor([0.9668, 0.9613, 0.9392]))
nms_ixs = torchvision.ops.nms(bbs, scores, iou_threshold=0.8)
nms_ixs
tensor([0])
bbs, labels = bbs[nms_ixs], labels[nms_ixs]
bbs = [unnorm(bb, img.shape[:2]) for bb in bbs]
plot_anns(img, (labels, bbs))
plt.show()

Ahora puedes intentar entrenar este modelo para el resto de imágenes del dataset. Es posible aplicar transfer learning, sustituyendo nuestra bakcbone por una red preentrenada (por ejemplo resenet) y sacando las cabezas de detecciones de los diferentes mapas de características intermedios (puedes añadir capas extras para seguir reduciendo la dimensionalidad como en la implementación original).
Resumen
En este post hemos aprendido a implementar un modelo de detección de objetos desde cero, inspirándonos en el modelo SSD. En primer lugar, hemos definido un conjunto de cajas que durante el entrenamiento nuestra red utilizará para detectar objetos. La salida de la red neuronal nos dará unos offsets sobre estas cajas a la vez que la distribución de probabilidad sobre todos los posibles objetos. Utilizamos la métric IoU para determinar qué cajas se parecen más a las anotaciones, y optimizar para sólo este conjunto. Por último, utilizamos el algorimto NMS para eliminar duplicados a la hora de generar predicciones.