mayo 12, 2021
~ 18 MIN
Self-Supervised Learning
< Blog RSSSelf-Supervised Learning
Hasta ahora hemos visto un montón de ejemplos y aplicaciones de redes neuronales, y en todas ellas hemos utilizado el mismo algoritmo de aprendizaje: el aprendizaje supervisado. Este tipo de aprendizaje se caracteriza por el acceso a un conjunto de datos etiquetado, consistente en pares de ejemplos de entradas y salidas. Un ejemplo muy sencillo de entender es el entrenamiento de un clasificador de imágenes, por ejemplo usando el dataset MNIST, que está compuesto por un conjunto de imágenes y cada una de ellas viene acompañada por su correspondiente etiqueta. Esto nos permite comparar para cada imagen del dataset la salida de nuestra red con la etiqueta real, el ground truth, y ajustar los parámetros internos del modelo de manera iterativa para que, poco a poco, las salidas sean lo más parecidas a las etiquetas.
Si bien este proceso es muy utilizado y ha dado muy buenos resultados en muchas aplicaciones, existen muchas otras en las que tales datasets etiquetados simplemente no existen o son escasos debido al coste y la complejidad de elaborarlos. Un ejemplo es el entrenamiento de redes neuronales para tareas de visión artificial en imágenes de satélite. Si queremos, por ejemplo, un detector de coches para calcular la ocupación de aparcamientos necesitaremos, primero, comprar imágenes de alta resolución (que pueden llegar a costar varios miles de euros cada una) y, segundo, etiquetar todos los coches que encontremos en las imágenes (lo cual puede llevar un buen rato). Es en este punto en el que nos preguntamos: ¿es posible entrenar redes neuronales sin etiquetas, solo a partir de datos? A este campo se le conoce como aprendizaje no supervisado, unsupervised learning en inglés, y es lo que vamos a explorar en este y los siguientes posts.
La analogía del pastel de Yan Lecun
Uno de los investigadores más influyentes en el ámbito del aprendizaje no supervisado, y del mundo del aprendizaje profundo en general, es Yann Lecun. Para entender la potencia de esta forma de aprendizaje presentó una analogía en la que, si el aprendizaje fuese un pastel, el aprendizaje supervisado solo correspondería al recubrimiento, mientras que el aprendizaje no supervisado sería el interior (y el aprendizaje por refuerzo, la cereza de arriba 😝)
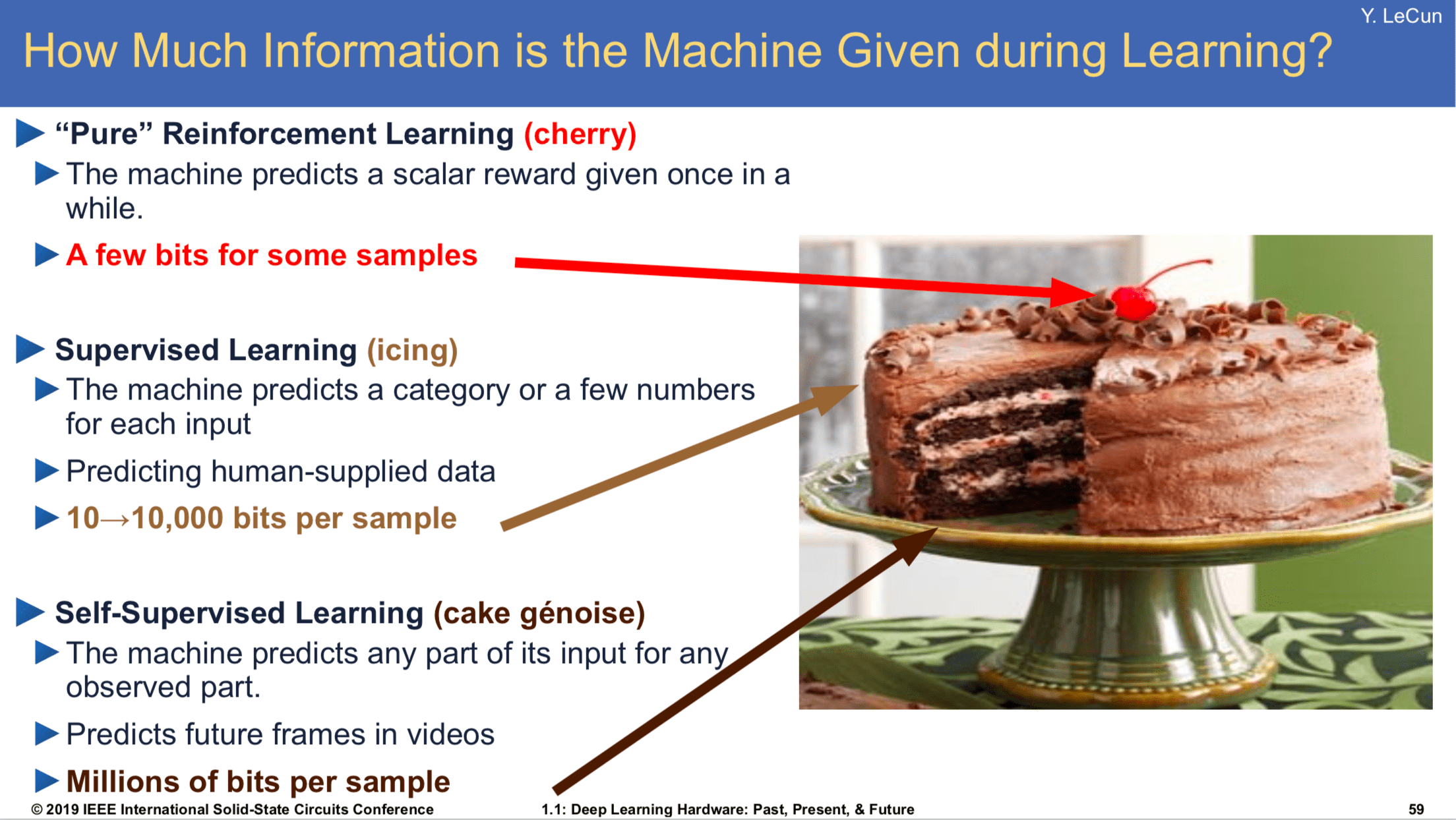
Esto nos da una idea de la importancia de ser capaces de entrenar nuestros modelos sin necesidad de un dataset etiquetado. Poder llevar a cabo este mecanismo de manera efectiva abriría la puerta a muchas aplicaciones hoy en día inconcebibles.
Si bien en el campo del machine learning existen diferentes algoritmos no supervisados, como algoritmos de clustering (K-Means, DBSCAN, ...), estimación de probabilidad (Gaussian Mixtures) o reducción de dimensionalidad (PCA y otros), los algoritmos no supervisados para deep learning son a día de hoy un tema de investigación muy activa, siendo los algoritmos de aprendizaje auto-supervisado (self-supervised learning) los más comunes por sus buenos resultados.
Self-Supervised Learning
La cuestión ahora es, ¿cómo podemos entrenar un modelo si no disponemos de etiquetas? En el caso del self-supervised learning, o aprendizaje auto-supervisado, este problema se resuelve con lo que se conoce como tarea pretexto, y consiste en utilizar el mismo input (o una versión distorsionada del mismo) como output. Ejemplos de estas tareas pueden ser la colorización (la entrada es una imagen en blanco y negro y el modelo debe dar a la salida la misma imagen en color), autoencoders (el modelo debe dar a la salida la misma entrada utilizando una versión comprimida de la misma), etc. La intuición tras estos métodos es que si un modelo es capaz de resolver la tarea pretexto es porque internamente será capaz de extraer las características visuales necesarias para, más tarde, poder hacer fine tuning para una tarea distinta, como la clasificación o detección de objetos.
En general, el self-supervised learning consiste en el entrenamiento de modelos que aprenden representaciones invariantes a distorsiones de la misma entrada. Esto significa que si un modelo es alimentado por una imagen en color y la misma imagen en blanco y negro, la representación interna (las features que nos daría el modelo justo antes del clasificador) debería ser igual, o lo más parecida posible. Diferentes métodos se basan en esta idea para construir, de una manera u otra, una función de pérdida que compare estas representaciones y minimize la diferencia entre pares de transformaciones que provengan de la misma imagen, mientras que maximice la diferencia entre imágenes diferentes. Algunos de los métodos más conocidos son:
En este post vamos a ver un ejemplo utilizando un método simple y reciente (al menos en el momento de elaborar este post): Barlow Twins.
CIFAR10
Para ilustrar la potencia del SSL vamos a entrenar primero una red neuronal convolucional sencilla para la clasificación de imágenes con el dataset CIFAR10 de manera supervisada, con ejemplos de imágenes y etiquetas.
import torch
import torchvision
import numpy as np
class Dataset(torch.utils.data.Dataset):
def __init__(self, train=True):
trainset = torchvision.datasets.CIFAR10(root='./data', train=train, download=True)
self.classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
self.imgs, self.labels = np.array([np.array(i[0]) for i in trainset]), np.array([i[1] for i in trainset])
def __len__(self):
return len(self.imgs)
def __getitem__(self, ix):
img = self.imgs[ix]
return torch.from_numpy(img / 255.).permute(2,0,1).float(), torch.tensor(self.labels[ix]).long()
ds = {
'train': Dataset(),
'test': Dataset(train=False)
}
ds['train'].imgs.shape, ds['test'].imgs.shape,
Files already downloaded and verified
Files already downloaded and verified
((50000, 32, 32, 3), (10000, 32, 32, 3))
batch_size = 1024
num_workers = 24
dl = {
'train': torch.utils.data.DataLoader(ds['train'], batch_size=batch_size, shuffle=True, num_workers=num_workers),
'test': torch.utils.data.DataLoader(ds['test'], batch_size=batch_size, shuffle=False, num_workers=num_workers)
}
imgs, labels = next(iter(dl['train']))
imgs.shape, labels.shape
(torch.Size([1024, 3, 32, 32]), torch.Size([1024]))
import matplotlib.pyplot as plt
fig = plt.figure(dpi=200)
c, r = 6, 4
for j in range(r):
for i in range(c):
ix = j*c + i
ax = plt.subplot(r, c, ix + 1)
img, label = imgs[ix], labels[ix]
ax.imshow(img.permute(1,2,0))
ax.axis('off')
plt.tight_layout()
plt.show()
import torch.nn.functional as F
class Model(torch.nn.Module):
def __init__(self, n_outputs=10, pretrained=False):
super().__init__()
self.backbone = torch.nn.Sequential(*list(torchvision.models.resnet18(pretrained=pretrained).children())[:-1])
if pretrained:
for param in self.backbone.parameters():
param.requires_grad = False
self.head = torch.nn.Sequential(
torch.nn.Flatten(),
torch.nn.Linear(512, n_outputs)
)
def forward(self, x):
x = self.backbone(x)
x = self.head(x)
return x
model = Model()
output = model(torch.randn(32, 3, 32, 32))
output.shape
torch.Size([32, 10])
from tqdm import tqdm
def step(model, batch, device):
x, y = batch
x, y = x.to(device), y.to(device)
y_hat = model(x)
loss = F.cross_entropy(y_hat, y)
acc = (torch.argmax(y_hat, axis=1) == y).sum().item() / y.size(0)
return loss, acc
def train(model, dl, optimizer, epochs=10, device="cuda"):
model.to(device)
hist = {'loss': [], 'acc': [], 'test_loss': [], 'test_acc': []}
for e in range(1, epochs+1):
# train
model.train()
l, a = [], []
bar = tqdm(dl['train'])
for batch in bar:
optimizer.zero_grad()
loss, acc = step(model, batch, device)
loss.backward()
optimizer.step()
l.append(loss.item())
a.append(acc)
bar.set_description(f"training... loss {np.mean(l):.4f} acc {np.mean(a):.4f}")
hist['loss'].append(np.mean(l))
hist['acc'].append(np.mean(a))
# eval
model.eval()
l, a = [], []
bar = tqdm(dl['test'])
with torch.no_grad():
for batch in bar:
loss, acc = step(model, batch, device)
l.append(loss.item())
a.append(acc)
bar.set_description(f"testing... loss {np.mean(l):.4f} acc {np.mean(a):.4f}")
hist['test_loss'].append(np.mean(l))
hist['test_acc'].append(np.mean(a))
# log
log = f'Epoch {e}/{epochs}'
for k, v in hist.items():
log += f' {k} {v[-1]:.4f}'
print(log)
return hist
model = Model()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
hist = train(model, dl, optimizer, epochs=3)
training... loss 1.5088 acc 0.4568: 100%|██████████| 49/49 [00:03<00:00, 15.51it/s]
testing... loss 2.1386 acc 0.3147: 100%|██████████| 10/10 [00:01<00:00, 9.05it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 1/3 loss 1.5088 acc 0.4568 test_loss 2.1386 test_acc 0.3147
training... loss 1.0689 acc 0.6151: 100%|██████████| 49/49 [00:03<00:00, 15.54it/s]
testing... loss 1.2041 acc 0.5877: 100%|██████████| 10/10 [00:01<00:00, 9.03it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 2/3 loss 1.0689 acc 0.6151 test_loss 1.2041 test_acc 0.5877
training... loss 0.8552 acc 0.6959: 100%|██████████| 49/49 [00:03<00:00, 15.64it/s]
testing... loss 1.1732 acc 0.6032: 100%|██████████| 10/10 [00:01<00:00, 8.97it/s]
Epoch 3/3 loss 0.8552 acc 0.6959 test_loss 1.1732 test_acc 0.6032
import pandas as pd
def plot_hist(hist):
fig = plt.figure(figsize=(10, 3), dpi=100)
df = pd.DataFrame(hist)
ax = plt.subplot(1, 2, 1)
df[['loss', 'test_loss']].plot(ax=ax)
ax.grid(True)
ax = plt.subplot(1, 2, 2)
df[['acc', 'test_acc']].plot(ax=ax)
ax.grid(True)
plt.show()
plot_hist(hist)
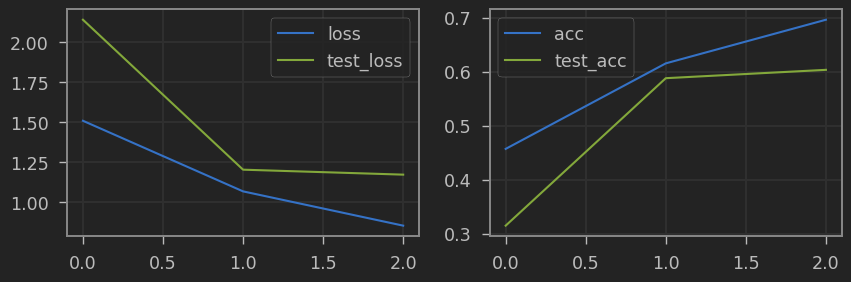
Tras el entrenmaiento llegamos a una precisión del 70%, lo cual podemos mejorar si entrenamos más epochs o con un mejor modelo (pero no es el objetivo de este post). Es importante remarcar que hemos enternado un modelo desde cero, y nuestro dataset consiste de 50000 imágenes de entrenamiento, lo cual no es una cantidad enorme. Sabemos de ejmplos anteriores que podemos usar el transfer learning para mejorar estos resultados, usando una red que haya sido pre-entrenada en otro dataset mucho más grande pudiendo aprovechar sus pesos como inicialización para nuestro problema. Lo más normal es utilizar redes pre-entrenada en el dataset Imagenet, ¿pero qué ocurre si nuestro dataset no consiste en imágene naturales o simplemente es muy diferente a Imagenet como es éste caso? Y más importante, ¿qué pasaría si tuviésemos incluso menos ejemplos de los que tenemos? Vamos a ilustrar este caso entrenando el mismo modelo con diferentes porcentajes de ejemplos por cada clase.
class Dataset(torch.utils.data.Dataset):
def __init__(self, train=True, pctg=1.):
trainset = torchvision.datasets.CIFAR10(root='./data', train=train, download=True)
self.classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
self.imgs, self.labels = np.array([np.array(i[0]) for i in trainset]), np.array([i[1] for i in trainset])
if pctg < 1.:
unique_labels = list(range(len(self.classes)))
filtered_imgs, filtered_labels = [], []
for lab in unique_labels:
ixs = (self.labels == lab)
lim = int(ixs.sum()*pctg)
filtered_imgs += self.imgs[ixs][:lim].tolist()
filtered_labels += self.labels[ixs][:lim].tolist()
self.imgs, self.labels = np.array(filtered_imgs), np.array(filtered_labels)
def __len__(self):
return len(self.imgs)
def __getitem__(self, ix):
img = self.imgs[ix]
return torch.from_numpy(img / 255.).permute(2,0,1).float(), torch.tensor(self.labels[ix]).long()
ds = {
'train': Dataset(pctg=0.01),
'test': Dataset(train=False)
}
Files already downloaded and verified
Files already downloaded and verified
fig, ax = plt.subplots(dpi=50)
ax.hist(ds['train'].labels, bins=10)
plt.show()
pctgs = [0.01, 0.1, 1.]
batch_size = 1024
epochs=3
lr=1e-3
hists = []
for pctg in pctgs:
ds = {
'train': Dataset(pctg=pctg),
'test': Dataset(train=False)
}
dl = {
'train': torch.utils.data.DataLoader(ds['train'], batch_size=batch_size, shuffle=True, num_workers=num_workers),
'test': torch.utils.data.DataLoader(ds['test'], batch_size=batch_size, shuffle=False, num_workers=num_workers)
}
model = Model()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
hist = train(model, dl, optimizer, epochs=epochs)
hists.append(hist)
Files already downloaded and verified
Files already downloaded and verified
training... loss 2.5636 acc 0.0900: 100%|██████████| 1/1 [00:00<00:00, 1.09it/s]
testing... loss 2.2918 acc 0.1177: 100%|██████████| 10/10 [00:01<00:00, 9.23it/s]
0%| | 0/1 [00:00<?, ?it/s]
Epoch 1/3 loss 2.5636 acc 0.0900 test_loss 2.2918 test_acc 0.1177
training... loss 1.5218 acc 0.5340: 100%|██████████| 1/1 [00:00<00:00, 1.07it/s]
testing... loss 2.2998 acc 0.1095: 100%|██████████| 10/10 [00:01<00:00, 9.20it/s]
0%| | 0/1 [00:00<?, ?it/s]
Epoch 2/3 loss 1.5218 acc 0.5340 test_loss 2.2998 test_acc 0.1095
training... loss 0.8678 acc 0.8280: 100%|██████████| 1/1 [00:00<00:00, 1.10it/s]
testing... loss 2.3001 acc 0.1079: 100%|██████████| 10/10 [00:01<00:00, 9.13it/s]
Epoch 3/3 loss 0.8678 acc 0.8280 test_loss 2.3001 test_acc 0.1079
Files already downloaded and verified
Files already downloaded and verified
training... loss 2.2472 acc 0.2310: 100%|██████████| 5/5 [00:01<00:00, 4.36it/s]
testing... loss 2.3309 acc 0.0997: 100%|██████████| 10/10 [00:01<00:00, 9.16it/s]
0%| | 0/5 [00:00<?, ?it/s]
Epoch 1/3 loss 2.2472 acc 0.2310 test_loss 2.3309 test_acc 0.0997
training... loss 1.5239 acc 0.4519: 100%|██████████| 5/5 [00:01<00:00, 4.49it/s]
testing... loss 2.5242 acc 0.0998: 100%|██████████| 10/10 [00:01<00:00, 9.15it/s]
0%| | 0/5 [00:00<?, ?it/s]
Epoch 2/3 loss 1.5239 acc 0.4519 test_loss 2.5242 test_acc 0.0998
training... loss 1.0692 acc 0.6277: 100%|██████████| 5/5 [00:01<00:00, 4.31it/s]
testing... loss 2.7783 acc 0.1072: 100%|██████████| 10/10 [00:01<00:00, 9.18it/s]
Epoch 3/3 loss 1.0692 acc 0.6277 test_loss 2.7783 test_acc 0.1072
Files already downloaded and verified
Files already downloaded and verified
training... loss 1.4852 acc 0.4636: 100%|██████████| 49/49 [00:03<00:00, 15.55it/s]
testing... loss 1.9736 acc 0.3617: 100%|██████████| 10/10 [00:01<00:00, 9.15it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 1/3 loss 1.4852 acc 0.4636 test_loss 1.9736 test_acc 0.3617
training... loss 1.0535 acc 0.6253: 100%|██████████| 49/49 [00:03<00:00, 15.51it/s]
testing... loss 1.3515 acc 0.5382: 100%|██████████| 10/10 [00:01<00:00, 9.19it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 2/3 loss 1.0535 acc 0.6253 test_loss 1.3515 test_acc 0.5382
training... loss 0.8577 acc 0.6954: 100%|██████████| 49/49 [00:03<00:00, 15.52it/s]
testing... loss 1.1203 acc 0.6048: 100%|██████████| 10/10 [00:01<00:00, 9.14it/s]
Epoch 3/3 loss 0.8577 acc 0.6954 test_loss 1.1203 test_acc 0.6048
fig = plt.figure(figsize=(8, 3), dpi=100)
ax = plt.subplot(1, 2, 1)
for i, pctg in enumerate(pctgs):
ax.plot(hists[i]['test_loss'])
ax.grid(True)
ax.legend(pctgs)
ax.set_title('loss')
ax = plt.subplot(1, 2, 2)
for i, pctg in enumerate(pctgs):
ax.plot(hists[i]['test_acc'])
ax.grid(True)
ax.set_title('acc')
plt.tight_layout()
plt.show()
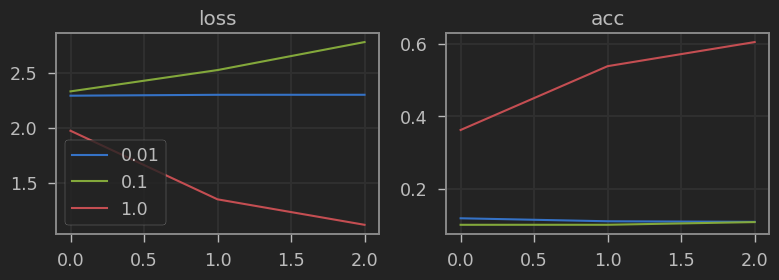
Como cabría esperar, cuantos más ejemplos de cada clase tengamos en el dataset, mejor resultados obtendremos. Sin embargo, nos gustaría poder tener una mejor eficiencia de datos (tener mejores resultados con menos ejemplos). Para ello, sabemos que necesitamos una red pre-entrenada capaz de extraer buenas características visuales desde el principcio. Vamos a comprar los resultados con una red pre-entrenada en Imagenet.
hists = []
for pctg in pctgs:
ds = {
'train': Dataset(pctg=pctg),
'test': Dataset(train=False)
}
dl = {
'train': torch.utils.data.DataLoader(ds['train'], batch_size=batch_size, shuffle=True, num_workers=num_workers),
'test': torch.utils.data.DataLoader(ds['test'], batch_size=batch_size, shuffle=False, num_workers=num_workers)
}
model = Model(pretrained=True)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
hist = train(model, dl, optimizer, epochs=epochs)
hists.append(hist)
Files already downloaded and verified
Files already downloaded and verified
training... loss 2.8241 acc 0.1000: 100%|██████████| 1/1 [00:00<00:00, 1.10it/s]
testing... loss 2.3807 acc 0.1021: 100%|██████████| 10/10 [00:01<00:00, 9.08it/s]
0%| | 0/1 [00:00<?, ?it/s]
Epoch 1/3 loss 2.8241 acc 0.1000 test_loss 2.3807 test_acc 0.1021
training... loss 2.5952 acc 0.1060: 100%|██████████| 1/1 [00:00<00:00, 1.12it/s]
testing... loss 2.3522 acc 0.1112: 100%|██████████| 10/10 [00:01<00:00, 9.20it/s]
0%| | 0/1 [00:00<?, ?it/s]
Epoch 2/3 loss 2.5952 acc 0.1060 test_loss 2.3522 test_acc 0.1112
training... loss 2.4698 acc 0.0960: 100%|██████████| 1/1 [00:00<00:00, 1.11it/s]
testing... loss 2.3340 acc 0.1243: 100%|██████████| 10/10 [00:01<00:00, 9.27it/s]
Epoch 3/3 loss 2.4698 acc 0.0960 test_loss 2.3340 test_acc 0.1243
Files already downloaded and verified
Files already downloaded and verified
training... loss 2.5440 acc 0.1031: 100%|██████████| 5/5 [00:01<00:00, 4.90it/s]
testing... loss 2.2951 acc 0.1326: 100%|██████████| 10/10 [00:01<00:00, 9.10it/s]
0%| | 0/5 [00:00<?, ?it/s]
Epoch 1/3 loss 2.5440 acc 0.1031 test_loss 2.2951 test_acc 0.1326
training... loss 2.3246 acc 0.1669: 100%|██████████| 5/5 [00:00<00:00, 5.07it/s]
testing... loss 2.2461 acc 0.1787: 100%|██████████| 10/10 [00:01<00:00, 9.28it/s]
0%| | 0/5 [00:00<?, ?it/s]
Epoch 2/3 loss 2.3246 acc 0.1669 test_loss 2.2461 test_acc 0.1787
training... loss 2.1528 acc 0.2245: 100%|██████████| 5/5 [00:00<00:00, 5.08it/s]
testing... loss 2.1852 acc 0.2241: 100%|██████████| 10/10 [00:01<00:00, 9.19it/s]
Epoch 3/3 loss 2.1528 acc 0.2245 test_loss 2.1852 test_acc 0.2241
Files already downloaded and verified
Files already downloaded and verified
training... loss 2.0244 acc 0.2920: 100%|██████████| 49/49 [00:01<00:00, 26.48it/s]
testing... loss 1.7801 acc 0.3935: 100%|██████████| 10/10 [00:01<00:00, 9.39it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 1/3 loss 2.0244 acc 0.2920 test_loss 1.7801 test_acc 0.3935
training... loss 1.7012 acc 0.4168: 100%|██████████| 49/49 [00:01<00:00, 27.42it/s]
testing... loss 1.6779 acc 0.4227: 100%|██████████| 10/10 [00:01<00:00, 9.23it/s]
0%| | 0/49 [00:00<?, ?it/s]
Epoch 2/3 loss 1.7012 acc 0.4168 test_loss 1.6779 test_acc 0.4227
training... loss 1.6268 acc 0.4414: 100%|██████████| 49/49 [00:01<00:00, 26.33it/s]
testing... loss 1.6328 acc 0.4392: 100%|██████████| 10/10 [00:01<00:00, 9.22it/s]
Epoch 3/3 loss 1.6268 acc 0.4414 test_loss 1.6328 test_acc 0.4392
fig = plt.figure(figsize=(8, 3), dpi=100)
ax = plt.subplot(1, 2, 1)
for i, pctg in enumerate(pctgs):
ax.plot(hists[i]['test_loss'])
ax.grid(True)
ax.legend(pctgs)
ax.set_title('loss')
ax = plt.subplot(1, 2, 2)
for i, pctg in enumerate(pctgs):
ax.plot(hists[i]['test_acc'])
ax.grid(True)
ax.set_title('acc')
plt.tight_layout()
plt.show()
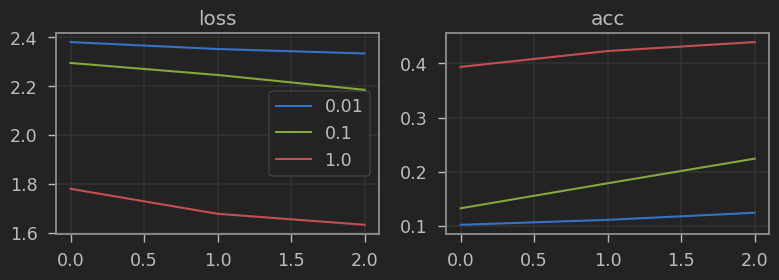
Nuestra eficiencia ha mejorado, aún así vemos que si usamos el 100% de los datos los resultados empeoran. Para este caso concreto, hacer fine tuning de toda la red mejoraría la métrica (usamos la backbone congelada para poder comparar con los resultados posteriores).
Si no queremos (o en función de la aplicación incluso no podremos) usar una red pre-entrenada en Imagenet, tendremos que pre-entrenar una red en imágenes propias de nuestra aplicación (en este caso CIFAR, pero puedes pensar en cualquier otra aplicación) de manera no supervisada. Vamos a implementar un ejemplo usando el método de Barlow Twins.
Lo primero que necesitamos es un dataset que nos de pares de imágenes con diferentes transformaciones. Durante el entrenamiento, calcularemos la salida de nuestro modelo para cada par de imágenes forzando la representación de las mismas a ser iguales. En el caso del método de Barlow Twins, ésto se consigue claculando la matriz de correlación cruzada entre los outputs y haciendo que se acerce lo más posible a la matriz identidad. Puedes ver más detalles en el artículo original.

import torch
import torchvision
class SSLDataset(torch.utils.data.Dataset):
def __init__(self, trans):
self.trans = trans
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True)
self.imgs = np.array([np.array(i[0]) for i in trainset])
def __len__(self):
return len(self.imgs)
def __getitem__(self, ix):
img = self.imgs[ix]
img1 = self.trans(image=img)['image']
img2 = self.trans(image=img)['image']
return torch.from_numpy(img1 / 255.).permute(2,0,1).float(), torch.from_numpy(img2 / 255.).permute(2,0,1).float()
import albumentations as A
trans = A.Compose([
A.RandomResizedCrop(32, 32),
A.HorizontalFlip(p=0.5),
A.ColorJitter(p=0.3),
A.ToGray(p=0.3),
#A.GaussianBlur(),
A.Solarize(p=0.3)
])
SSLds = SSLDataset(trans)
Files already downloaded and verified
import matplotlib.pyplot as plt
import random
ix = random.randint(0, len(SSLds))
img1, img2 = SSLds[ix]
fig = plt.figure(dpi=50)
ax = plt.subplot(1, 2, 1)
ax.imshow(img1.permute(1,2,0))
ax.axis('off')
ax = plt.subplot(1, 2, 2)
ax.imshow(img2.permute(1,2,0))
ax.axis('off')
plt.tight_layout()
plt.show()

En cuanto al modelo, éste estará formado por una backbone (la misma que usarmos más tarde para hacer fine tuning) y un perceptrón multicapa con varias capas (que luego tiraremos a la basura ya que solo nos interesa la bakbone).
class SSLModel(torch.nn.Module):
def __init__(self, f=512):
super().__init__()
self.backbone = torch.nn.Sequential(*list(torchvision.models.resnet18().children())[:-1])
self.head = torch.nn.Sequential(
torch.nn.Flatten(),
torch.nn.Linear(512, f),
torch.nn.BatchNorm1d(f),
torch.nn.ReLU(),
torch.nn.Linear(f, f),
torch.nn.BatchNorm1d(f),
torch.nn.ReLU(),
torch.nn.Linear(f, f)
)
def forward(self, x):
x = self.backbone(x)
x = self.head(x)
return x
SSLmodel = SSLModel()
output = SSLmodel(torch.randn(32, 3, 32, 32))
output.shape
torch.Size([32, 512])
Para evaluar el resultado durante el entrenamiento, entrenaremos un nuevo modelo sobre la backbone pre-entrenada de manera supervisada cada cierto número de epochs.
import copy
class FTModel(torch.nn.Module):
def __init__(self, backbone='SSLbackbone.pt', n_outputs=10):
super().__init__()
self.backbone = torch.jit.load(backbone)
for param in self.backbone.parameters():
param.requires_grad = False
self.head = torch.nn.Sequential(
torch.nn.Flatten(),
torch.nn.Linear(512, n_outputs)
)
def forward(self, x):
x = self.backbone(x)
x = self.head(x)
return x
from tqdm import tqdm
def SSLeval(SSLmodel):
torch.jit.script(SSLmodel.backbone.cpu()).save('SSLbackbone.pt')
ds = {
'train': Dataset(),
'test': Dataset(train=False)
}
batch_size = 1024
dl = {
'train': torch.utils.data.DataLoader(ds['train'], batch_size=batch_size, shuffle=True, num_workers=num_workers),
'test': torch.utils.data.DataLoader(ds['test'], batch_size=batch_size, shuffle=False, num_workers=num_workers)
}
FTmodel = FTModel('SSLbackbone.pt')
optimizer = torch.optim.Adam(FTmodel.parameters(), lr=1e-3)
hist = train(FTmodel, dl, optimizer, epochs=3)
return hist['acc'][-1], hist['test_acc'][-1]
def SSLstep(model, batch, device, l=5e-3):
# two randomly augmented versions of x
x1, x2 = batch
x1, x2 = x1.to(device), x2.to(device)
# compute representations
z1 = model(x1)
z2 = model(x2)
# normalize repr. along the batch dimension
N, D = z1.shape
z1_norm = (z1 - z1.mean(0)) / z1.std(0) # NxD
z2_norm = (z2 - z2.mean(0)) / z2.std(0) # NxD
# cross-correlation matrix
c = (z1_norm.T @ z2_norm) / N # DxD
# loss
c_diff = (c - torch.eye(D, device=device)).pow(2) # DxD
# multiply off-diagonal elems of c_diff by lambda
d = torch.eye(D, dtype=bool)
c_diff[~d] *= l
return c_diff.sum()
def SSLtrain(model, dl, optimizer, scheduler, epochs=10, device="cuda", eval_each=10):
hist = {'loss': [], 'acc': [], 'test_acc': []}
for e in range(1, epochs+1):
model.to(device)
# train
model.train()
l, a = [], []
bar = tqdm(dl)
for batch in bar:
optimizer.zero_grad()
loss = SSLstep(model, batch, device)
loss.backward()
optimizer.step()
l.append(loss.item())
bar.set_description(f"training... loss {np.mean(l):.4f}")
hist['loss'].append(np.mean(l))
scheduler.step()
# log
log = f'Epoch {e}/{epochs}'
for k, v in hist.items():
if len(v) > 0:
log += f' {k} {v[-1]:.4f}'
print(log)
# eval
if not e % eval_each:
print("evaluating ...")
val_train_acc, val_test_acc = SSLeval(model)
hist['acc'].append(val_train_acc)
hist['test_acc'].append(val_test_acc)
return hist
SSLdl = torch.utils.data.DataLoader(SSLds, batch_size=1024, shuffle=True, num_workers=num_workers)
SSLmodel = SSLModel()
optimizer = torch.optim.Adam(SSLmodel.parameters(), lr=1e-4)
epochs = 500
scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, pct_start=0.01, max_lr=0.1, total_steps=epochs, verbose=True)
hist = SSLtrain(SSLmodel, SSLdl, optimizer, scheduler, epochs=epochs)
fig = plt.figure(figsize=(8, 3), dpi=100)
ax = plt.subplot(1, 2, 1)
for i, pctg in enumerate(pctgs):
ax.plot(ssl_hists[i]['test_loss'], label=f'{pctg} (ssl)')
ax.grid(True)
ax.legend()
ax.set_title('loss')
ax = plt.subplot(1, 2, 2)
for i, pctg in enumerate(pctgs):
ax.plot(ssl_hists[i]['test_acc'])
ax.grid(True)
ax.set_title('acc')
plt.tight_layout()
plt.show()
# 12, 22, 44
# 13, 28, 60
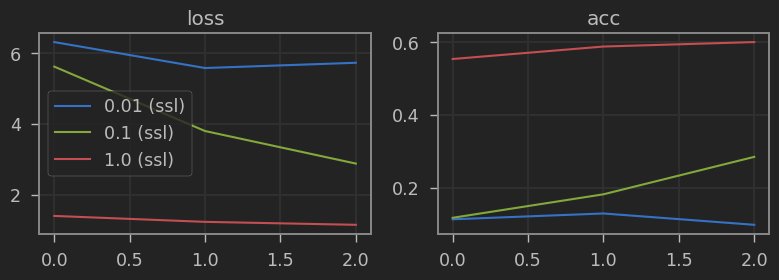
¡Estupendo! Nuestro modelo es ligeramente mejor que si usamos los pesos entrenados de Imagenet, pero el hecho de que sea al menos comparable ya es una muy buena noticia. Además, nos da mucho mejor resultado si usamos el 1% o 10% de las etiquetas comparado con el modelo entrenado desde cero. Puedes usar esta técnica a partir de ahora cuando tengas un dataset anotado pequeño pero dispongas de muchos más ejemplos sin anotar, o te sea fácil conseguirlos. Tus modelos mejorarán considerablemente.
Resumen
Disponer de una red pre-entrenada capaz de extraer representaciones útiles para tareas de visión por computador nos da una eficiencia de datos mucho mayor, requiriendo de menos datos etiquetados y menor coste computacional para obtener resultados aceptables. Si bien lo más común es utilizar una red pre-entrenada con el dataset Imagenet, existen muchas aplicaciones en las que las características visuales de las imágenes son diferentes (como por ejemplo imágenes médicas o por satélite). En estos casos, el tener redes pre-entrenadas en los datos propios del dominio de aplicación nos puede dar muchos mejores resultados. Además, en estas aplicaciones en particular, elaborar datasets de calidad y con muchos ejemplos es muy costoso. Tener modelos capaces de dar buenos resultados con pocas muestras nos da mucha ventaja. El campo self-supervised learning se enfoca precisamente en resolver estos problemas y cada vez más podemos ver que se utiliza en el pre-entrenamiento de redes neuronales enormes con datasets no etiquetas consistenes en millones de millones de muestras, que luego son fine tuneadas a tareas concretas con datasets etiquetados dando mejores resultados que si tuviésemos que entrenar desde cero.
Recursos
Aprende más sobre SSL con estos vídeos: