Las ecuaciones de Euler

En este post vamos a resolver las ecuaciones de Euler con redes neuronales.

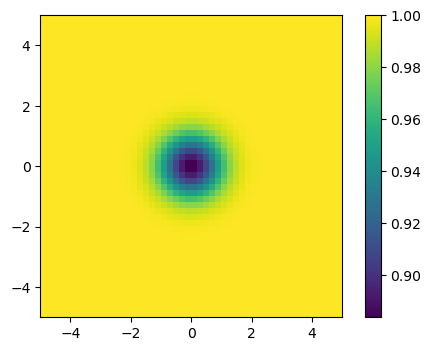
Para ello resolveremos el problema del vórtice isentrópico, un vórtice en un dominio cuadrado periódico el cual es arrastrado por una corriente libre. Las ecuaciones de Euler son una simplificación de las ecuaciones de Navier Stokes, en las que no se considera la viscosidad de un fluido (por lo que son aplicables a fluidos muy poco viscosos, como el aire). Debido a esto, nuestro vórtice deberá ser arrastrado por la corriente sin verse alterado ya que la convección será el único mecanismo en juego. Este caso es muy útil para evaluar diferentes métodos numéricos y sus propiedades.

import math
import torch

# condición inicial

GAMMA = 1.4
b = 5

x = torch.linspace(-5,5,50)
y = torch.linspace(-5,5,50)
xx, yy = torch.meshgrid(x,y)

r2 = xx**2 + yy**2
r0 = (1-(b*(GAMMA-1))/(8*math.pi*math.pi*GAMMA)*torch.exp(1-r2))**(1/(GAMMA-1))
u0 = 1 - b/(2*math.pi)*torch.exp(0.5*(1-r2))*y
v0 = b/(2*math.pi)*torch.exp(0.5*(1-r2))*x
p0 = r0**GAMMA

import matplotlib.pyplot as plt

plt.figure(dpi=100)
plt.imshow(r0, vmin=r0.min(), vmax=r0.max(), origin='lower', extent=[-5, 5, -5 ,5])
plt.colorbar()
plt.show()

def computeGrads(y, x):
    grads, = torch.autograd.grad(y, x, grad_outputs=y.data.new(y.shape).fill_(1), create_graph=True, only_inputs=True)
    return grads

import torch.nn as nn

class Sine(nn.Module):
    def __init__(self):
        super().__init__()
    def forward(self, x):
        return torch.sin(x)

mlp = nn.Sequential(
    nn.Linear(3, 100),
    Sine(),
    nn.Linear(100, 100),
    Sine(),
    nn.Linear(100, 100),
    Sine(),
    nn.Linear(100, 4)
)

device = "cuda"

mlp.to(device)

Sequential(
  (0): Linear(in_features=3, out_features=100, bias=True)
  (1): Sine()
  (2): Linear(in_features=100, out_features=100, bias=True)
  (3): Sine()
  (4): Linear(in_features=100, out_features=100, bias=True)
  (5): Sine()
  (6): Linear(in_features=100, out_features=4, bias=True)
)

from fastprogress.fastprogress import progress_bar

N_STEPS = 100000
N_SAMPLES = 1000
N_SAMPLES_0 = 1000

optimizer = torch.optim.Adam(mlp.parameters())
scheduler =  torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[int(0.4*N_STEPS), int(0.8*N_STEPS)], gamma=0.1)
criterion = torch.nn.MSELoss()
mlp.train()


mlp.to(device)

mb = progress_bar(range(1, N_STEPS+1))

for step in mb:

    # optimize for PDE
    x = torch.rand(N_SAMPLES, device=device)*10. - 5.
    y = torch.rand(N_SAMPLES, device=device)*10. - 5.
    t = torch.rand(N_SAMPLES, device=device)*10.

    X = torch.stack([
        x,
        y,
        t
    ], axis=-1)
    X.requires_grad = True

    y_hat = mlp(X)
    r, u, v, p = y_hat[:,0], y_hat[:,1], y_hat[:,2], y_hat[:,3]

    grads = computeGrads(r, X)
    drdt = grads[:, 2]

    grads = computeGrads(r*u, X)
    drudx, drudt = grads[:, 0], grads[:, 2]

    grads = computeGrads(r*v, X)
    drvdy, drvdt = grads[:, 1], grads[:, 2]

    grads = computeGrads(r*u*u + p, X)
    druupdx = grads[:, 0]

    grads = computeGrads(r*u*v, X)
    drvudx, druvdy = grads[:, 0], grads[:, 1]

    grads = computeGrads(r*v*v + p, X)
    drvvpdy = grads[:, 1]

    re = p/(GAMMA-1) + 0.5*r*(u*u + v*v)
    grads = computeGrads(re, X)
    dredt = grads[:, 2]

    grads = computeGrads((re+p)*u, X)
    drepudx = grads[:, 0]

    grads = computeGrads((re+p)*v, X)
    drepvdy = grads[:, 1]

    pde_loss = criterion(drdt, - drudx - drvdy) + \
        criterion(drudt, - druupdx - druvdy) + \
        criterion(drvdt, - drvudx - drvvpdy) + \
        criterion(dredt, - drepudx - drepvdy)

    # initial condition
    r2 = x**2 + y**2
    r00 = (1-(b*(GAMMA-1))/(8*math.pi*math.pi*GAMMA)*torch.exp(1-r2))**(1/(GAMMA-1))
    u = 1 - b/(2*math.pi)*torch.exp(0.5*(1-r2))*y
    v = b/(2*math.pi)*torch.exp(0.5*(1-r2))*x
    p = r00**GAMMA

    X = torch.stack([
        x,
        y,
        torch.zeros(N_SAMPLES, device=device)
    ], axis=-1)
    X.requires_grad = True
    y_hat = mlp(X)
    ini_loss = criterion(y_hat, torch.stack([
        r00,
        u,
        v,
        p
    ], axis=-1))

    # optimize for boundary conditions
    # left
    Y0 = torch.stack([
        -5.*torch.ones(N_SAMPLES_0, device=device),
        y,
        t
    ], axis=-1)
    # right
    Y1 = torch.stack([
        5.*torch.ones(N_SAMPLES_0, device=device),
        y,
        t,
    ], axis=-1)
    y0 = mlp(Y0)
    y1 = mlp(Y1)
    y_loss = criterion(y0, y1)
    # bot
    X0 = torch.stack([
        x,
        -5.*torch.ones(N_SAMPLES_0, device=device),
        t
    ], axis=-1)
    # right
    X1 = torch.stack([
        x,
        5.*torch.ones(N_SAMPLES_0, device=device),
        t,
    ], axis=-1)
    x0 = mlp(X0)
    x1 = mlp(X1)
    x_loss = criterion(x0, x1)

    bound_loss = y_loss + x_loss

    # update
    optimizer.zero_grad()
    loss = ini_loss + bound_loss + pde_loss
    loss.backward()
    optimizer.step()
    scheduler.step()

    mb.comment = f'pde_loss {pde_loss.item():.5f} ini_loss {ini_loss.item():.5f} bound_loss {bound_loss.item():.5f}'

import numpy as np

def run_mlp(Nx, Ny, dt, tf):
    ps, ts = [], []
    t = 0
    x = np.linspace(-5,5,Nx)
    y = np.linspace(-5,5,Ny)
    X = np.stack(np.meshgrid(x,y), -1).reshape(-1, 2)
    X0 = torch.from_numpy(X).float()
    mlp.eval()
    mlp.cpu()
    while t < tf:
        with torch.no_grad():
            X = torch.cat([  # N, (X, Y, T)
                X0,
                torch.ones(len(X0)).unsqueeze(1)*t,
            ], axis=1)
            p = mlp(X)
        ps.append(p[:,0].reshape(Ny,Nx))
        ts.append(t)
        t += dt
    return ps, ts

from matplotlib import animation, rc
rc('animation', html='html5')

def update(i):
    r = ps[i]
    ax.clear()
    ax.imshow(r, vmin=0.9, vmax=1., origin='lower', extent=[-5, 5, -5 ,5])
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_title(f't = {ts[i]:.3f}')
    ax.axis('off')
    return ax

ps, ts = run_mlp(33, 33, 0.2, 10)

fig = plt.figure(dpi=100)
ax = plt.subplot(1,1,1)
anim = animation.FuncAnimation(fig, update, frames=len(ps), interval=200)
plt.close()

anim

Como puedes ver la solución aproximada mediante la red neuronal sigue el comportamiento esperado.

Resumen

En este post, y los anteriores, hemos aprendido a resolver ecuaciones diferenciales utilizando redes neuronales en vez de métodos numéricos tradicionales. Ésto tiene sus ventajas, pero también sus desventajas. Aún así, es un campo muy prometedor con el potencial de revolucionar el campo de la simulación física.

A diferencia de los métodos tradicionales, las redes neuronales nos dan soluciones continuas y derivables, que no están limitadas por fenómenos físicos y que permiten añadir los parámteros libres como parte del proceso de búsqueda de la solución (por lo que una vez entrenada la red, nos da soluciones para un gran rango de situaciones diferentes, acelerando el proceso de optimización).

Por otro lado, el entrenamiendo de las redes es lento y la solución que nos da, si bien es más flexible, sigue estando limitado al rango de situaciones que haya visto durante el entrenamiento.

Creo que la solución ganadora será una hibridación de métodos tradicionales con redes neuronales, de la misma forma que ocurre en el campo del aprendizaje por refuerzo u otras disciplinas científicas que el deep learning está revolucionando.