Cálculo Numérico

En ocasiones, a la hora de resolver un problema matemático, podemos derivar una fórmula que provee de una descripción simbólica de la solución. Sin embargo, en muchos otros casos como la mayoría de algoritmos de Machine Learning y Deep Learning, esto no es posible y la solución solo puede aproximarse mediante técnicas iterativas con unos requisitos de cómputo que crecen con el tamaño del problema. Es por este motivo que necesitamos súper-ordenadores con miles y miles de procesadores para resolver problemas como predicción meteorológica, diseño de nuevos medicamentos o entrenar grandes redes neuronales. Algunas operaciones que tienen lugar durante este proceso iterativo son la resolución de sistemas de ecuaciones lineales o la optimización de algunos valores dadas unas restricciones, por poner algunos ejemplos. El campo de las matemáticas que se dedica al estudio de la resolución de este tipo de problemas es el cálculo numérico.

Precisión Numérica

La principal dificultad que nos encontramos a la hora de llevar a cabo cálculos matemáticos en un ordenador digital es la necesidad de representar cualquier valor numérico con un conjunto de bits finito. Esto implica que para casi cualquier valor numérico tendremos un error en su representación. Esto puede ser problemático cuando llevamos a cabo muchas operaciones con valores que presentan este problema, ya que los errores pueden irse acumulando dando como resultado una solución errónea. Podemos ver esto con el siguiente ejemplo en el que tenemos un vector de números enteros no negativos representados por 8 bits (lo que implica que sólo podemos representar valores entre 0 y 255). Esta es la representación típica de los píxeles en una imágen. Supongamos que queremos aumentar el brillo de la imágen, para ello vamos a sumar una cantidad determinada a todos los píxeles de la imágen.

import numpy as np

x = np.array([0, 100, 255], dtype=np.uint8)
x

array([  0, 100, 255], dtype=uint8)

# overflow

x + 1

array([  1, 101,   0], dtype=uint8)

Como puedes ver, el valor 255 ha pasado a ser de 0 en vez de 256. Esto es porque con 8 bits no podemos representar ningún valor por encima de 255, por lo que el siguiente valor (255 + 1) es el primero (0). Esto implica que nuestro objetivo, que era aumentar el brillo de la imágen, sólo ha funcionado para algunos píxeles, mientras que en el resto observamos justo el efecto contrario (ahora se han oscurecido). Este fenómeno se conoce como integer overflow, pero puede ocurrir con cualquier tipo de valor numérico y dirección.

# underflow

x - 1

array([255,  99, 254], dtype=uint8)

Veamos otro ejemplo utilizando la función softmax, detallada en este post.

def softmax(z):
    return np.exp(z)/sum(np.exp(z))

Si calculamos el resultado para un vector de valores constantes, el resultado que esperamos es siendo la longitud del vector.

x = np.full(5, 1)

softmax(x)

array([0.2, 0.2, 0.2, 0.2, 0.2])

Si estos valores son muy grandes, calcular su exponencial dará como resultado un número todavía más grande corriendo el riesgo de incurrir en overflow y división entre 0.

x = np.full(5, 1e3)

softmax(x)

RuntimeWarning: overflow encountered in exp

RuntimeWarning: invalid value encountered in true_divide






array([nan, nan, nan, nan, nan])

Esto implica que pese a que utilicemos la función softmax en muchas de nuestras aplicaciones tenemos que utilizar una implementación alternativa que evitaremos este problema. Para este caso, una implementación más estable es la siguiente

def softmax_estable(z):
    z = z - np.max(z)
    return np.exp(z)/sum(np.exp(z))

x = np.full(5, 1)

softmax_estable(x)

array([0.2, 0.2, 0.2, 0.2, 0.2])

x = np.full(5, 1e10)

softmax_estable(x)

array([0.2, 0.2, 0.2, 0.2, 0.2])

Restando el valor máximo a nuestro vector conseguimos que el número más grande sea siempre 0, evitando tanto el overflow como el underflow obteniendo el mismo resultado. Este es sólo un ejemplo para ilustrar el hecho de que en cálculo numérico en ocasiones es necesario modificar las expresiones que utilizamos para prevenir errores debido a la finita representación de nuestros valores. Esto es algo muy común que veremos en muchas librerías de Machine Learning y Deep Learning.

Optimización

La mayoría de algoritmos de Deep Learning requieren de optimización de una manera u otra. Esto se refiere a la tarea de minimizar o maximizar una función objetivo cambiando . En el caso de la minimización, la función objetivo también se conoce con los nombre de función de coste, función de pérdida o función de error (o loss function en inglés). En cualquier caso siempre nos referimos a lo mismo.

Optimización basada en Gradientes

Existen muchos algoritmos de optimización, pero en el caso del Deep Learning el más común es la optimización basada en gradientes. En este caso utilizaremos la derivada de la función de coste con respecto a los parámetros que queremos cambiar para definir la regla que usaremos para variar estos parámetros. Considera la función de coste representada en la siguiente figura.

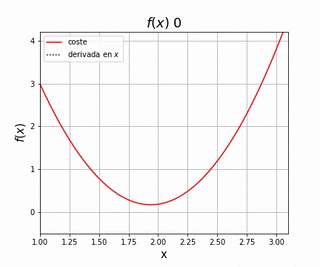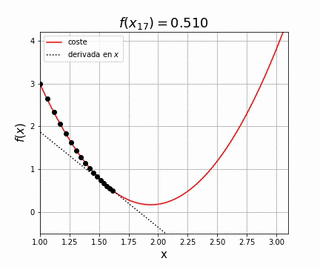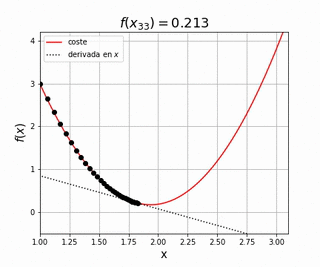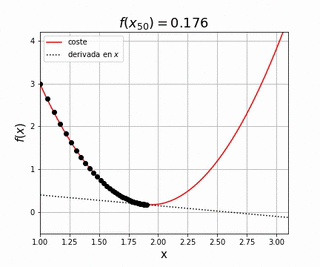
Nuestro objetivo es encontrar el valor de que resulta en el valor más pequeño posible de , su valor mínimo. Para ello podemos utilizar la derivada de la función , representada por la línea punteada. Esta derivada nos indica la pendiente de la función en el punto , por lo que si queremos minimizar tendremos que cambiar en la dirección de pendiente negativa, es decir aquella que haga que disminuya. Imagina que dejamos una pelota encima de una superficie similar a la representada por . Lo que observaremos es que la pelota empieza a moverse en la dirección de pendiente negativa debido a la fuerza de la gravedad. Utilizamos este símil para entender como podemos utilizar el gradiente de una función para su optimización. Matemáticamente

donde es una constante pequeña. Así pues, conociendo podemos actualizar el valor de con la siguiente sencilla regla

donde se conoce como el ratio de aprendizaje, o learning rate en inglés. Este método se conoce por el nombre de descenso por gradiente, o gradient descent en inglés, y es el método más utilizado hoy en día en el entrenamiento de redes neuronales. En futuros posts entraremos mucho más detalle en cómo funciona el algoritmo, aplicándolo en multitud de modelos diferentes, viendo el efecto que tiene el learning rate y otras variantes existentes que se construyen por encima con el objetivo de acelerar el proceso de convergencia, encontrar este valor mínimo lo más rápido posible. Por ahora es suficiente con entender cómo funciona el algoritmo de descenso por gradiente a alto nivel: calcularemos la derivada de una función de coste con respecto a los parámetros que queremos optimizar, los cuales iremos variando de manera iterativa siempre en la dirección de mayor pendiente negativa.

Un aspecto a destacar muy importante del algoritmo de descenso por gradiente es que no nos asegura encontrar siempre el óptimo global de la función de coste, sino que puede quedarse "atascado" en óptimos locales. Esto dependerá de la forma que tenga la función de coste y de la inicialización. Es habitual inicial los parámetros de un modelo de manera aleatoria, lo que implica que podemos ejecutar el mismo proceso varias veces, encontrando diferentes soluciones.

Por suerte, en espacios de muy alta dimensionalidad (cuando optimizamos con respecto a muchísimos parámetros) es relativamente sencillo encontrar siempre una dirección en el espacio en el que el gradiente sea negativo, pudiendo escapar de estos óptimos locales convergiendo a resultados similares independientemente de la inicialización.

Más allá del gradiente

Si estás familiarizando con problemas de optimización es posible que conozcas el método de Newton, un método de optimización muy utilizado. Es posible utilizarlo también en la optimización de modelos de IA, sin embargo no es muy utilizado en la práctica. El motivo es porque normalmente estos modelos están formados por muchos parámetros (millones, incluso billones). El método de Newton, y otros métodos de optimización similares, están basados en la segunda derivada de la función, . Desde un punto de vista computacional, calcular estas segundas derivadas no es práctico (a veces incluso imposible debido a limitaciones de memoria). Es por este motivo que estos métodos de optimización de segundo orden no son tan utilizados cómo los métodos de primer orden que solo necesitan el cálculo de la primera derivada, como el algoritmo de descenso por gradiente.

Por otro lado también es común la optimización de funciones de coste respecto a un conjunto finito de parámetros, conocido como optimización con restricciones. Por ejemplo, queremos encontrar el valor mínimo de con la restricción < 1. Veremos más adelante como resolver estos casos, que normalmente consisten en añadir términos adicionales a la función de coste original que tengan en cuenta tales restricciones.

Resumen

En este post hemos introducido varios conceptos del cálculo numérico que utilizaremos muy a menudo en el desarrollo de algoritmos de Machine Learning. En primer lugar, al representar números reales en un ordenador con una capacidad de memoria limitada siempre incurrimos en errores de precisión que tenemos que tener en cuenta a la hora de diseñar nuestro algoritmos. Estos errores pueden acumularse operación tras operación dando resultados erróneos. Por otro lado, hemos introducido el concepto de optimización por gradiente, en el que calculamos la derivada de una función de coste con respecto a los parámetros de interés los cuales vamos variando siguiendo la regla del descenso por gradiente hasta encontrar nuestra solución óptima. Este es el método por defecto al entrenar redes neuronales, y al ser tan usado dedicaremos varios futuros posts para entenderlo en mucho más detalle.

Referencias

Libros

• Deep Learning (Goodfellow, Bengio y Courville, 2016)