El Perceptrón Multicapa - Clasificación

El Perceptrón Multicapa

En el post anterior hemos introducido el modelo de Perceptrón Multicapa, o MLP, la arquitectura de red neuronal más básica basada en el Perceptrón. Hemos visto cómo calcular la salida de un MLP de dos capas a partir de unas entradas y cómo encontrar los pesos óptimos para una tarea de regresión. En este post vamos a mejorar la implementación de nuestro MLP de dos capas para que sea capaz también de llevar a cabo tareas de clasificación.

Implementación

La mayoría del código que utilizaremos fue desarrollado para el Perceptrón y lo puedes encontrar en este post. Lo único que cambiaremos es la lógica del modelo, el resto de funcionalidad (funciones de pérdida, funciones de activación, etc, siguen siendo exactamente igual).

Funciones de activación

Para la capa oculta de nuestro MLP utilizaremos una función de activación de tipo relu, de la cual necesitaremos su derivada.

def relu(x):
  return np.maximum(0, x)

def reluPrime(x):
  return x > 0

En cuanto a las funciones de activación que utilizaremos a la salida del MLP, éstas son las que hemos introducido en posts anteriores:

• Lineal: usada para regresión (junto a la función de pérdida MSE).
• Sigmoid: usada para clasificación binaria (junto a la función de pérdida BCE).
• Softmax: usada para clasificación multiclase (junto a la función de pérdida crossentropy, CE).

def linear(x):
    return x

def sigmoid(x):
  return 1 / (1 + np.exp(-x))

def softmax(x):
    return np.exp(x) / np.exp(x).sum(axis=-1,keepdims=True)

Funciones de pérdida

Como acabamos de comentar en la sección anterior, estas son las funciones de pérdida que hemos visto hasta ahora para las diferentes tareas.

# Mean Square Error -> usada para regresión (con activación lineal)
def mse(y, y_hat):
    return np.mean((y_hat - y.reshape(y_hat.shape))**2)

# Binary Cross Entropy -> usada para clasificación binaria (con sigmoid)
def bce(y, y_hat):
    return - np.mean(y.reshape(y_hat.shape)*np.log(y_hat) - (1 - y.reshape(y_hat.shape))*np.log(1 - y_hat))

# Cross Entropy (aplica softmax + cross entropy de manera estable) -> usada para clasificación multiclase
def crossentropy(y, y_hat):
    logits = y_hat[np.arange(len(y_hat)),y]
    entropy = - logits + np.log(np.sum(np.exp(y_hat),axis=-1))
    return entropy.mean()

Y sus derivadas

def grad_mse(y, y_hat):
    return y_hat - y.reshape(y_hat.shape)

def grad_bce(y, y_hat):
    return y_hat - y.reshape(y_hat.shape)

def grad_crossentropy(y, y_hat):
    answers = np.zeros_like(y_hat)
    answers[np.arange(len(y_hat)),y] = 1    
    return (- answers + softmax(y_hat)) / y_hat.shape[0]

Implementación MLP

Ahora que ya tenemos definidas las diferentes funciones de activación y de pérdida que necesitamos, vamos a implementar nuestro MLP de dos capas capaz de llevar a cabo tanto tareas de regresión como de clasificación. Del mismo modo que ya hicimos con el Perceptrón, definiremos una clase base que servirá para la implementación de las clases particulares para cada caso.

# clase base MLP 

class MLP():
  def __init__(self, D_in, H, D_out, loss, grad_loss, activation):
    # pesos de la capa 1
    self.w1, self.b1 = np.random.normal(loc=0.0,
                                  scale=np.sqrt(2/(D_in+H)),
                                  size=(D_in, H)), np.zeros(H)
    # pesos de la capa 2
    self.w2, self.b2 = np.random.normal(loc=0.0,
                                  scale=np.sqrt(2/(H+D_out)),
                                  size=(H, D_out)), np.zeros(D_out)
    self.ws = []
    # función de pérdida y derivada
    self.loss = loss
    self.grad_loss = grad_loss
    # función de activación
    self.activation = activation

  def __call__(self, x):
    # salida de la capa 1
    self.h_pre = np.dot(x, self.w1) + self.b1
    self.h = relu(self.h_pre)
    # salida del MLP
    y_hat = np.dot(self.h, self.w2) + self.b2 
    return self.activation(y_hat)
    
  def fit(self, X, Y, epochs = 100, lr = 0.001, batch_size=None, verbose=True, log_each=1):
    batch_size = len(X) if batch_size == None else batch_size
    batches = len(X) // batch_size
    l = []
    for e in range(1,epochs+1):     
        # Mini-Batch Gradient Descent
        _l = []
        for b in range(batches):
            # batch de datos
            x = X[b*batch_size:(b+1)*batch_size]
            y = Y[b*batch_size:(b+1)*batch_size] 
            # salida del perceptrón
            y_pred = self(x) 
            # función de pérdida
            loss = self.loss(y, y_pred)
            _l.append(loss)        
            # Backprop 
            dldy = self.grad_loss(y, y_pred) 
            grad_w2 = np.dot(self.h.T, dldy)
            grad_b2 = dldy.mean(axis=0)
            dldh = np.dot(dldy, self.w2.T)*reluPrime(self.h_pre)      
            grad_w1 = np.dot(x.T, dldh)
            grad_b1 = dldh.mean(axis=0)
            # Update (GD)
            self.w1 = self.w1 - lr * grad_w1
            self.b1 = self.b1 - lr * grad_b1
            self.w2 = self.w2 - lr * grad_w2
            self.b2 = self.b2 - lr * grad_b2
        l.append(np.mean(_l))
        # guardamos pesos intermedios para visualización
        self.ws.append((
            self.w1.copy(),
            self.b1.copy(),
            self.w2.copy(),
            self.b2.copy()
        ))
        if verbose and not e % log_each:
            print(f'Epoch: {e}/{epochs}, Loss: {np.mean(l):.5f}')

  def predict(self, ws, x):
    w1, b1, w2, b2 = ws
    h = relu(np.dot(x, w1) + b1)
    y_hat = np.dot(h, w2) + b2
    return self.activation(y_hat)

# MLP para regresión
class MLPRegression(MLP):
    def __init__(self, D_in, H, D_out):
        super().__init__(D_in, H, D_out, mse, grad_mse, linear)

# MLP para clasificación binaria
class MLPBinaryClassification(MLP):
    def __init__(self, D_in, H, D_out):
        super().__init__(D_in, H, D_out, bce, grad_bce, sigmoid)

# MLP para clasificación multiclase
class MLPClassification(MLP):
    def __init__(self, D_in, H, D_out):
        super().__init__(D_in, H, D_out, crossentropy, grad_crossentropy, linear)

Vamos a probar ahora nuestra implementación para diferentes ejemplos.

Regresión

En primer lugar, vamos a replicar los resultados obtenidos en el post anterior para verificar que nuestro modelo de MLP sigue funcionando bien.

import numpy as np
import matplotlib.pyplot as plt

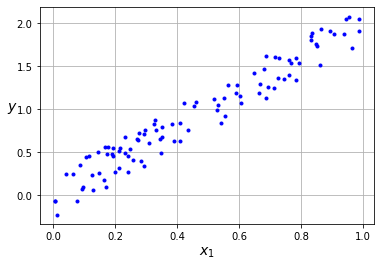
x = np.random.rand(100)
X = x.reshape(-1, 1)
y = 2*x + (np.random.rand(100)-0.5)*0.5

plt.plot(x, y, "b.")
plt.xlabel("$x_1$", fontsize=14)
plt.ylabel("$y$", rotation=0, fontsize=14)
plt.grid(True)
plt.show()

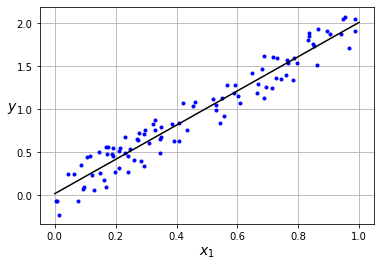
model = MLPRegression(D_in=1, H=3, D_out=1)
epochs, lr = 50, 0.01
model.fit(x.reshape(len(x),1), y, epochs, lr, log_each=10)

Epoch: 10/50, Loss: 0.07477
Epoch: 20/50, Loss: 0.04802
Epoch: 30/50, Loss: 0.03910
Epoch: 40/50, Loss: 0.03464
Epoch: 50/50, Loss: 0.03197

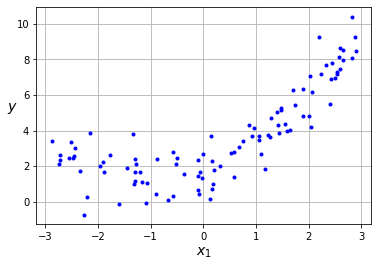
m = 100
x = 6 * np.random.rand(m, 1) - 3
y = 0.5 * x**2 + x + 2 + np.random.randn(m, 1)

plt.plot(x, y, "b.")
plt.xlabel("$x_1$", fontsize=14)
plt.ylabel("$y$", rotation=0, fontsize=14)
plt.grid(True)
plt.show()

model = MLPRegression(D_in=1, H=3, D_out=1)
epochs, lr = 50, 0.01
model.fit(x.reshape(len(x),1), y, epochs, lr, batch_size=1, log_each=10)

Epoch: 10/50, Loss: 1.44752
Epoch: 20/50, Loss: 1.26686
Epoch: 30/50, Loss: 1.20394
Epoch: 40/50, Loss: 1.16913
Epoch: 50/50, Loss: 1.14773

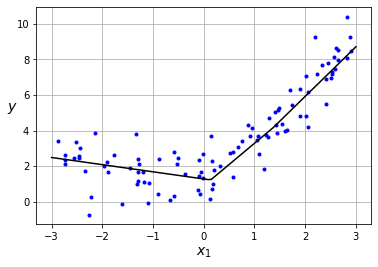
Como puedes observar nuestro MLP es capaz de ajustarse a datos que no sigan una distribución lineal. Ésta es la principal limitación del Perceptrón, es un modelo muy simple, y el MLP es capaz de solventar este problema (siempre y cuando usemos funciones de activación no lineales en la capa oculta. ¿Sabes por qué? Puedes encontrar la respuesta en el post anterior).

Clasificación Binaria

Ahora vamos a aplicar nuestro MLP al problema de clasificación binaria. Para ellos vamos a utilizar el dataset Iris, que ya conocemos de los posts anteriores de clasificación con el Perceptrón.

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data[:, (2, 3)]  # petal length, petal width
y = iris.target

X.shape, y.shape

((150, 2), (150,))

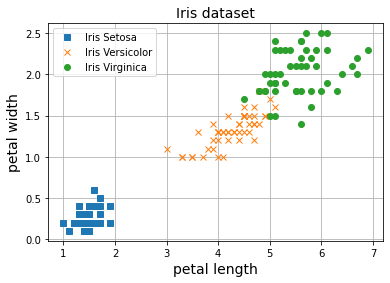
Este dataset contiene información sobre flores y el objetivo es clasificar en tres clases distintas. En esta sección vamos a intentar separar simplemente una de las clases del resto (clasificación binaria).

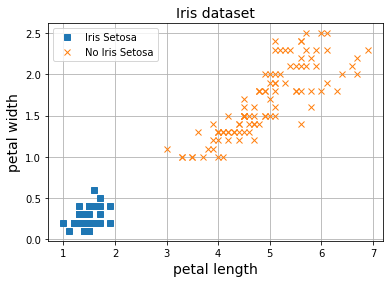
y = (iris.target == 0).astype(np.int)

model = MLPBinaryClassification(D_in=2, H=3, D_out=1)
epochs, lr = 50, 0.01

# normalización datos
X_mean, X_std = X.mean(axis=0), X.std(axis=0)
X_norm = (X - X_mean) / X_std

model.fit(X_norm, y, epochs, lr, batch_size=1, log_each=10)

Epoch: 10/50, Loss: -0.06950
Epoch: 20/50, Loss: -0.03924
Epoch: 30/50, Loss: -0.02738
Epoch: 40/50, Loss: -0.02107
Epoch: 50/50, Loss: -0.01714

Nuestro MLP es capaz de separar las clases sin problema. Si recuerdas, en el caso del Perceptrón, el modelo no era capaz de separar las flores de tipo Iris Versicolor del resto, ya que esta clase no es linealmente separable.

X = iris.data[:, (2, 3)]  # petal length, petal width
y = (iris.target == 1).astype(np.int)

X_mean, X_std = X.mean(axis=0), X.std(axis=0)
X_norm = (X - X_mean) / X_std

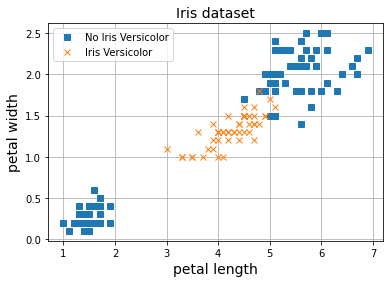
Sin embargo, nuestro nuevo modelo, el MLP, es capaz de solventar este problema.

model = MLPBinaryClassification(D_in=2, H=10, D_out=1)
epochs, lr = 50, 0.1
model.fit(X_norm, y, epochs, lr, batch_size=1, log_each=10)

Epoch: 10/50, Loss: 0.01092
Epoch: 20/50, Loss: 0.00305
Epoch: 30/50, Loss: -0.00065
Epoch: 40/50, Loss: -0.00291
Epoch: 50/50, Loss: -0.00443

Como puedes observar, el MLP es capaz de resolver el problema del Perceptrón, y es que cuantas más capas y neuronas por capas usemos, mayor capacidad de representación tendrá el modelo (las redes neuronales más grandes a día de hoy tienen varios Billones de conexiones).

Clasificación Multiclase

Por último vamos a ver cómo aplicar nuestro modelo para clasificación en multiples clases.

X = iris.data[:, (2, 3)]  # petal length, petal width
y = iris.target

X_mean, X_std = X.mean(axis=0), X.std(axis=0)
X_norm = (X - X_mean) / X_std

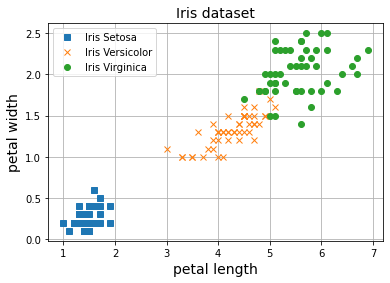
plt.plot(X[y==0, 0], X[y==0, 1], 's', label="Iris Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], 'x', label="Iris Versicolor")
plt.plot(X[y==2, 0], X[y==2, 1], 'o', label="Iris Virginica")
plt.grid()
plt.legend()
plt.xlabel('petal length', fontsize=14)
plt.ylabel('petal width', fontsize=14)
plt.title("Iris dataset", fontsize=14)
plt.show()

model = MLPClassification(D_in=2, H=10, D_out=3)
epochs, lr = 50, 0.2
model.fit(X_norm, y, epochs, lr, batch_size=10, log_each=10)

Epoch: 10/50, Loss: 0.44251
Epoch: 20/50, Loss: 0.34481
Epoch: 30/50, Loss: 0.27839
Epoch: 40/50, Loss: 0.23627
Epoch: 50/50, Loss: 0.20840

De nuevo, nuestro MLP es capaz de separar las tres clases en el dataset. En posts anteriores hemos trabajado también con el dataset MNIST para clasificación de imágenes en diez clases distintas. ¿Te ves capaz de utilizar nuestro MLP para resolver ese problema?

Resumen

En este post hemos visto como implementar un Perceptrón Multicapa en Python para tareas de regresión y clasificación. Como ya hicimos anteriormente para el caso del Perceptrón hemos validado nuestra implementación con el dataset de clasificación de flores Iris, tanto para clasificación binaria como multiclase. Sin embargo, nuestra implementación está muy limitada. ¿Qué pasa si queremos usar un MLP de más de dos capas?, ¿y si queremos usar una función de activación diferente a la relu en la capa oculta?, ¿podríamos utilizar un algoritmo de optimización diferente al descenso por gradiente? Para poder hacer todo esto necesitamos un framework más flexible, similar a lo que nos ofrecen Pytorch y Tensorflow. En el siguiente post desarrollaremos nuestro propio framework de MLP para que sea más flexible y que también nos servirá para entender cómo funcionan el resto de frameworks de redes neuronales por dentro.